Enunciado
Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 7.Problemas - Ex. 16
Se a função de Gibbs de um sistema deve decrescer durante qualquer processo espontâneo em que a temperatura e a pressão permanecem constantes, mostre que a entropia de um sistema isolado deve crescer durante um processo espontâneo.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears e Salinger se a função de Gibbs de um sistema deve decrescer durante qualquer processo espontâneo em que a temperatura e a pressão permanecem constantes, mostre que a entropia de um sistema isolado deve crescer durante um processo espontâneo.
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera para mostrar que a entropia do sistema isolado deve crescer durante um processo espontâneo temos que,
A variação de Gibbs pode ser relacionada com a variação na entalpia, ficando
O que pode ser reescrito como,
E como a temperatura se aproxima de zero com base no gráfico imposto por,
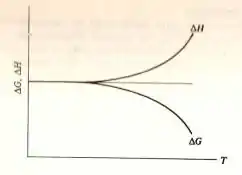
Com sua variação vai ser definida com,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
