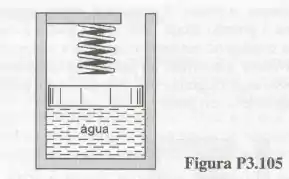
Inicialmente, o conjunto cilindro-pistão mostrado na Fig. P3.105 contém 1 litro de água a e com título igual a . O conjunto é aquecido e o pistão se movimenta. O volume interno do conjunto é no instante em que o pistão toca a mola linear. O aquecimento continua até que a pressão atinja . Sabendo que o diâmetro do pistão é e que a constante de mola é , calcule a temperatura na água no final do processo.

Sabemos que dividir o volume do recipiente por seu volume específico resulta na massa contida, portanto, vamos calcular o volume específico.

Olhando na tabela com a temperatura inicial , temos os seguintes volumes

Aproveitando que estamos olhando na tabela atrás dos volumes, vamos coletar a pressão também será útil no final, .

E a fórmula:

A diferença entre o volume de vapor e líquido constitui no volume da fase líquido vapor.

Aplicando na fórmula:

Com o volume específico em mãos e sabemos que o volume do recipiente é , substituindo no cálculo da massa, fica:

Para calcular o volume específico final temos que saber o volume específico do estado 2:

Como o primeiro processo e o segundo processo são proporcionais, quesito em volume, temos que:

Com a massa calculada vai enunciar a equação do somatório das pressões no estado 3:

é igual a , pois, no processo de expansão a pressão não se altera até encosta na mola.

Sendo que vai ser igual a:

Resultando em:

Só que pode ser determinar por:

Substituindo na conta:

Temos a equação que determinara nosso volume específico final.

Antes de aplicarmos fórmula, temos que calcular a área do pistão:

Aplicando as variáveis na fórmula, temos:

Olhando na tabela com a pressão de e a