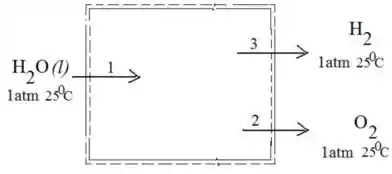
Um inventor desenvolveu um dispositivo que em regime permanente recebe água líquida a 25°C, 1 atm com uma vazão mássica de 4 kg/h e produz fluxos separados de hidrogênio (H2) e oxigênio (O2), cada qual a 25°C, 1 atm. O inventor afirma que o dispositivo requer uma potência elétrica de entrada de 237,180 kJ por kmol de H2 quando opera isotermicamente a 25°C. Ocorre transferência de calor com a vizinhança, mas os efeitos das energias cinética e potencial podem ser ignorados. Avalie a alegação do inventor.

É dado que:

• Taxa de vazão mássica da água:
• Potência elétrica de entrada:

A reação total da célula é

O balanço de energia do estado permanente é

O balanço de taxa de entropia a estado uniforme

Usando essa equação na achada anteriormente

A taxa de vazão mássica molar de

E

Temos que

Da tabela de propriedades termodinâmicas a e

Como sabemos

Então para satisfazer a equação que obtemos

O que é impossível

Então o valor para o valor de potência elétrica não está correta.