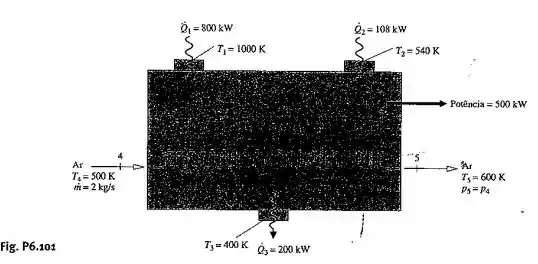
Um inventor forneceu os dados ilustrados na Fig. P6.101, para uma operação em regime permanente de um sistema de cogeração produzindo potência e aumentando a temperatura de uma corrente de ar. O sistema recebe e descarrega energia por transferência de calor que ocorrem estão indicados pelas setas correspondentes. O modelo de gás ideal pode ser aplicado para o ar. Os efeitos das energias cinética e potencial são desprezíveis. Utilizando os balanços de energia e de entropia, avalie o desempenho termodinâmico do sistema.
Passo 1
E aí, tudo bem?
Se ajeite aí e vem comigo resolver essa questão!
Começamos o nosso problema aplicando a equação de taxa de energia em nosso sistema desprezando os efeitos das energias cinética e potencial:
Pelas tabelas do Apêndice A, para o ar tratado como um gás ideal, devemos obter as seguintes propriedades:
- :
- :
Sendo:
Substituindo os dados:
O sistema está termodinamicamente equilibrado.
Passo 2
No estado estacionário, temos que a relação de entropia é dada por:
Assim:
Como possuímos uma geração de entropia negativa, temos que o sistema não se adequa a 2ª Lei da Termodinâmica, sendo assim, o sistema é impossível.