Uma mistura de gás com uma análise molar especificada entra em um compressor em uma taxa de fluxo de massa e estado especificados e sai em uma pressão especificada. A eficiência do compressor isentrópico também é conhecida. Determine a temperatura na saída, a potência necessária e a taxa de produção de entropia.
Passo 1
CONHECIDO: Os dados a seguir:
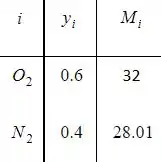
Passo 2
PREMISSAS: (1) O compressor está bem isolado e opera em estado estacionário. (2) Os efeitos da energia cinética e potencial podem ser ignorados. (s) A mistura segue as idealizações do modelo de Dalton e a composição permanece constante.
ANÁLISE: A temperatura T2 pode ser determinada usando isentrópico ou eficiência, mas primeiro a temperatura no estado 2s, ,, deve ser encontrada. uma vez que, Eq. 12,36 pode ser invocado para escrever
Consequentemente, com 3 ∘ dados das tabelas de gases ideais
resolvendo iterativamente usando dados da tabela, T25 = 470k.
Passo 3
De acordo com as suposições listadas, o efeito do compressor isentrópico é
Então
Consequentemente
Ou
Passo 4
Resolvendo
O poder requerido está
Em que m é o peso molecular da mistura. Em que Dessa forma
Os balanços da massa e da taxa de entropia reduzem no estado estacionário para dar
Portanto
Com dados da tabela A23
Uma solução iterativa com dados de tabela pode ser evitada usando 1T. Os resultados para T2s, T2, W Cv e σcv obtidos usando IT concordam com os valores dados aqui.