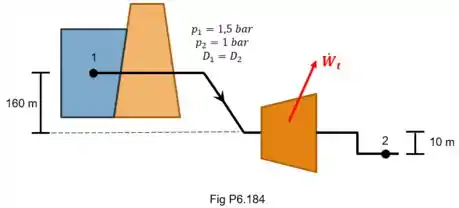
Como mostrado na Fig. P6.184, água escoa a partir de um reservatório elevado através de uma turbina hidráulica, operando em regime permanente. Determine a potência máxima de saída, em MW, associada à vazão mássica de 950 kg/s. Os diâmetros de entrada e saída são iguais. A água pode ser modelada com incompressível com . A aceleração da gravidade local é de 9,8 m/s².
Passo 1
Faaaala pessoal! Vamos fazer mais essa questão?

Começando organizando algumas hipóteses para prosseguirmos com os cálculos:
1 – Para o volume de controle tem apenas uma entrada, em 1, e apenas uma saída, em 2, e compreende a turbina.
2 – O processo ocorre em regime permanente.
3 – A água será tratada como incompressível.
Vamos organizar também os dados fornecidos!
Agora vamos para os cálculos!
Passo 2
Você concorda que no caso ideal, que não acontece, sem irreversibilidades, a potência real que sairia da turbina seria igual a potencia ideal? E caso existam irreversibilidades, a potência real gerada pela turbina seria menor que a ideal?
Tendo assim:
Nós temos que o trabalho de um processo reversível pode ser dado por:
Se , então !
E como a água é incompressível nesse caso !
Podemos reorganizar da seguinte forma o trabalho real:
Opa!!! Já temos todos os valores, né? Que beleza!
Passo 3
Agora é só substituir!
Ou seja, o valor máximo que a turbina pode gerar é 1,54 MW!
Tranquilo né? Vamos para a próxima!