Mostrando todos os passos importantes, deduza: (a) as Eqs. 13.41a e 13.41b; (b) Eqs. 13.44a e 13.44b.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Aplicando os balanços de taxa de massa e energia para a entrada e saída do reator
Para as mesmas temperaturas na entrada e saída
Aplicando o balanço de taxa de energia
Para , temos que
Passo 3
Substituindo o resultado encontrado na equação
Então, a exergia química máxima é
Somando as contribuições de cada um dos componentes, a exergia química por mol é
Passo 4
b) o diagrama abaixo mostra o reator usado para a exergia química padrão de
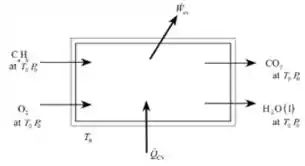
Passo 5
Para o combustível de hidrocarboneto puro em e
A reação é
O balanço de taxa de exergia para o volume de controle é
Para sem irreversibilidades
Exergia química do
Resposta
Ei, a resposta está no passo a passo :)