Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 174
O motor de e 1.800 rpm de um compressor esta queimado e deve ser substituído ou por um motor padrão com eficiência de a plena carga e custo de ou por um motor com alta eficiência de e custo de . O compressor opera durante a plena carga, e sua operacao a carga parcial e desprezível. Considerando que o custo da eletricidade e de , determine a quantidade de energia e o dinheiro economizados por essa instalação com a compra do motor de alta eficiência em vez da utilização do motor padrão. Determine também se a economia do motor de alta eficiência justifica a diferença de preço, já que o motor tem uma expectativa de vida útil de . Ignore todos os possíveis descontos da empresa de energia local.
Passo 1
Vamos lá! A questão nos afirma que o motor de um compressor de é queimado e deve ser substituído ou por um motor padrão de de eficiência ou por um motor de alta eficiência de . A quantidade de energia e dinheiro que a instalação economizará com a compra do motor de alta eficiência em vez do motor padrão deve ser determinada. Também deve ser determinado se a poupança do motor de alta eficiência justifica o diferencial de preço.
Podemos representar como,
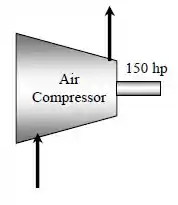
Assumindo que:
- O compressor funciona a plena carga quando em funcionamento.
- A vida útil dos motores é de .
- Não há descontos envolvidos.
- O preço da eletricidade permanece constante.
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que as economias de energia e de custos associadas à instalação do motor de alta eficiência neste caso são determinados a ser
Passo 3
Já a poupança de custo é dada por:
O custo adicional do motor energeticamente eficiente é