Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 194

As necessidades de água quente de uma residência são atendidas por um aquecedor elétrico de água de 60 L, com potência nominal de 1,6 kW. O tanque de água quente inicialmente está cheio de água quente a 80ºC. Alguém toma um banho misturando uma vazão constante de água quente do tanque com uma vazão de 0,06 kg/s de água frias a 20ºC. Após um banho de 8 min, a temperatura de água no tanque é medida, verificando-se que caiu para 60ºC. O aquecedor permaneceu ligado durante o banho, e a água quente retirada do tanque foi substituída pela mesma vazão de água fria. Determine o fluxo de massa de água quente retirada do tanque durante o banho e a temperatura média da água misturada utilizada para o banho.

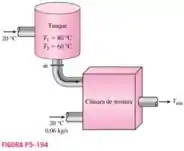
Passo 1

Vamos primeiro analisar o tanque:

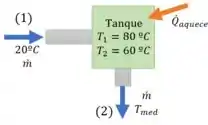
Ao longo dos 8 minutos do banho a temperatura sai de 80 º C para 60 º C . Então também podemos considerar que ao longo do banho a temperatura fornecida pelo tanque é igual a temperatura média:

T m e d = 80 + 60 2 = 70 º C

Também podemos calcular a massa de água no tanque:

m t a n q u e = V ⋅ ρ = 60 L ⋅ 1 k g L = 60   k g

Se fizermos a consideração de que o regime é permanente e que a massa de saída é igual a massa de entrada, podemos fazer o balanço de energia. Onde a variação de energia é referente a diferença de temperatura do tanque em 8 minutos; a energia que entra é relacionada a massa que entra em (1) e o calor do aquecedor; e a massa que sai é a (2)

Δ E = E e n t r a - E s a i

Q Δ t = E 1 + Q a q u e c e - E 2

m t a n q u e c p Δ T Δ t = m ˙ h 1 + Q a q u e c e - m ˙ h 2

m t a n q u e c p T 2 - T 1 Δ t = m ˙ h 1 - h 2 + Q a q u e c e

Podemos simplificar a entalpia utilizando calor específico:

m t a n q u e c p T 2 - T 1 Δ t = m ˙ c p T 1 - T m e d + Q a q u e c e

Isolando a vazão mássica:

m ˙ = m t a n q u e c p T 2 - T 1 Δ t ⋅ c p T 1 - T m e d - Q a q u e c e c p T 1 - T m e d

m ˙ = m t a n q u e T 2 - T 1 Δ t ⋅ T 1 - T m e d - Q a q u e c e c p T 1 - T m e d

Aplicando os valores:

m ˙ = 60   k g ⋅ ( 60 - 80 ) 8 ⋅ 60   s ⋅ ( 20 - 70 ) - 1,6 4,18 ⋅ 20 - 70

m ˙ = 0,0577 k g s  

Passo 2

Agora vamos analisar a câmara de mistura:

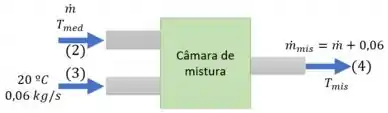
Fazendo o balanço de energias:

Δ E = E e n t r a - E s a i

Para o caso da câmara de mistura, consideramos que ela está em estado permanente, e que a variação de energia é nula:

E e n t r a = E s a i

m ˙ 2 c p T m e d + m 3 c p T 3 = m m i s c p T m i s

0,0577 k g s ⋅ 343   K + 0,06 k g s ⋅ 293   K = 0,0577 + 0,6 k g ⋅ T m i s

T m i s = 0,0577 k g s ⋅ 343   K + 0,06 k g s ⋅ 293   K 0,0577 + 0,6 k g

T m i s = 0,0577 k g s ⋅ 343   K + 0,06 k g s ⋅ 293   K 0,0577 + 0,6 k g

T m i s = 317,5   K

T m i s = 44,51   º C

Resposta

m ˙ = 0,0577 k g s  

T m i s = 44,51   º C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Vapor a 60 psia e 350ºF é misturado continuamente com água a 40ºF e 60 psia em um dispositivo adiabático. Vapor entra no dispositivo a uma taxa de 0.05 lbm/s, enquanto a água entra a 1 lbm/s. Determin
Dois fluxos de massa do mesmo gás ideal são misturadosem uma câmara com escoamento em regime permanente enquanto recebem energia por transferência de calor da vizinhança. O processo de mistura ocorre
Considere um processo de mistura com escoamento em regime permanente. Sob quais condições a energia transportada para o volume de controle pelas correntes de entrada será igual à energia transportada
Quando duas correntes de fluido se misturam em uma câmara de mistura, é possível que a temperatura da mistura seja mais baixa do que a temperatura de ambas as correntes? Explique.
Uma corrente de água quente a 80 °C entra em uma câmara de mistura com um fluxo de massa de 0,5 kg/s, onde é misturada com outra corrente de água fria a 20 °C. Para que a mistura saia da câmara a 42 °