Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 1.Problemas - Ex. 86

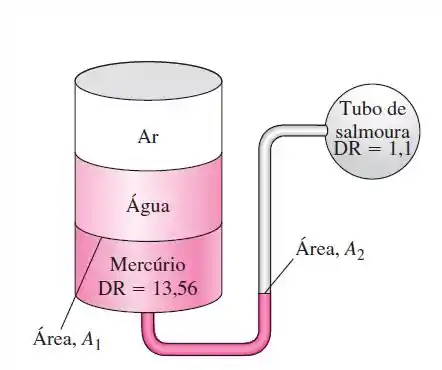
Observe o sistema mostrado na figura. Considerando que a interface salmoura-mercúrio na coluna da direita se desloca 5   m m para baixo devido a uma variação de 0,7   k P a na pressao do ar, com a pressão no tubo de salmoura constante, determine a razão A 2 / A 1 .

Passo 1

Considerando os pesos específicos para mercúrio D R = 13,56 , para salmoura D R = 1,1 e para água densidade ρ = 1000   k g / m 3 .

Considerando que todos os fluidos são incompreensíveis e a pressão do ar é insignificante.

Iremos começar com a pressão do ar percorrendo o tubo pela água e iremos somar os termos ρ g h como vamos descendo do tubo e subtraindo assim que subirmos algum termo e igualaremos a pressão do tubo de salmoura.

Vamos considerar pressão do ar como P a e pressão do tubo de salmoura P b .

Fica esperto que aqui teremos duas equações, uma antes da variação e uma após.

Passo 2

Antes:

P a 1 + ρ h 2 o g h h 2 o + ρ H g g h H g 1 - ρ s a l g h s a l 1 = P b

Depois:

P a 2 + ρ h 2 o g h h 2 o + ρ H g g h H g 2 - ρ s a l g h s a l 2 = P b

Como pressão no tubo de salmoura é constante P b das duas equações são equivalentes. Subtraindo depois e antes:

Perceba que os termos dos h , possuem Δ devido h f i n a l - h i n i c i a l .

P a 2 - P a 1 + ρ H g g Δ h H g - ρ s a l g Δ h s a l = 0

P a 2 - P a 1 ρ h 2 o g = D R H g Δ h H g - D R s a l Δ h s a l = 0 (1)

Passo 3

Temos que P a 2 - P a 1 = - 0,7   k P a = - 700   N / m 2 e que   Δ h s a l = 0,005   m .

Preste atenção aqui, perceba que temos um aumento de nível do mercúrio do lado direito oque origina nosso A 2 e um subnível devido o aumento do próprio mercúrio oque origina nosso A 1 , perceba que por mais que ocorram estes desníveis o volume do mercúrio permanece constante, ou seja:

A 1 Δ h H g , e s q u e r d a   = A 2 Δ h H g ,   d i r e i t a

Portanto:

Δ h H g , T O T A L   = Δ h H g ,   d i r e i t a + Δ h H g , e s q u e r d a   = Δ h s a l + Δ h s a l A 2 / A 1

= Δ h s a l 1 + A 2 A 1

Substituindo os valores na equação (1):

700 1000 ∙ 9,8   = [ 13,56 ∙ 0,005 ∙ 1 + A 2 A 1 - 1,1 ∙ 0,005 ]

A 2 A 1 = 0,134  

Resposta

A 2 A 1 = 0,134  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pressão em uma linha de agua e de 1 500k P a . Como essa pressão seria expressa em ( a ) unidades l b / p é 2 é e ( b ) unidades l b f / p o l 2 ( p s i )?
A pressão manométrica de um liquido a uma profundidade de 3   m e lida como 42   k P a . Determine a pressão manométrica do mesmo liquido a uma profundidade de 9   m .
A pressão do hélio dentro de um balão de brinquedo e de 1 250m mH g . Como essa pressao seria expressa em k P a ?
A pressão a saída de um compressor de ar e de 150p s i a . Como essa pressão seria expressa em k P a ?
Expresse a lei de Pascal e de um exemplo pratico para ela.