Uma panela de pressão é uma panela que cozinha alimento muito mais rápido que panelas comuns, mantendo pressão e temperatura elevadas durante o cozimento. A pressão dentro da panela é controlada por um regulador de pressão (a válvula) que mantém a pressão a um nível constante, periodicamente permitindo algum vapor escapar – e, desse modo, evitando qualquer acumulação de excesso de pressão. Panelas de pressão, em geral, mantém uma pressão manométrica de 2 atm (ou 3 atm absoluto) no interior. Portanto, panelas de pressão cozinham a uma temperatura de cerca de 133 °C em vez de 100 °C, reduzindo em aproximadamente 70% o tempo de cozimento e também minimizando a perda de nutrientes. As panelas de pressão mais recentes usam uma válvula de mola com várias configurações de pressão – ao contrário das mais antigas que usam um peso sobre a tampa.

O volume de uma determinada panela de pressão corresponde a 6 L, e sua pressão manométrica de operação é de 75 kPa. Inicialmente, a panela contém 1 kg de água. Após a panela ter atingido a pressão de operação, calor é fornecido para ela a uma taxa de 500 W durante 30 min. Considerando uma pressão atmosférica de 100 kPa, determine (a) a temperatura na qual ocorre o cozimento e (b) a quantidade de água deixada na panela de pressão no final do processo

Durante o processo de cozimento, dentro da panela temos uma mistura de líquido saturado e de vapor saturado. Então, vamos usar a Tabela A-5:

Para resolver a questão vamos ter que imaginar dois instantes:

O instante (1) se dá no instante exato em que a pressão atinge , neste instante, a panela de pressão contém uma mistura de vapor saturado e líquido saturado e nenhuma massa saiu da panela.

O instante (2) se dá ao fim do cozimento, quando uma parte significativa da massa escapou em forma de vapor, mas a pressão continua em e a panela ainda contém uma mistura saturada.

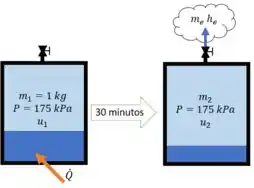
Sabemos que parte da massa de água escapa pela válvula. Então vamos chamar a massa que escapa de e a massa final na panela de :

Fazemos o balanço de energia:

A variação de energia corresponde a variação de energia interna entre o instante (1) e o instante (2). A energia que entra é o calor fornecido para a panela ao longo do tempo, e a energia que sai é o fluxo de massa que escapa da panela:

Vamos usar a tabela A-5 para determinar a entalpia e a energia interna

Primeiro, observe que o vapor que escapa da panela é vapor saturado à . Então:

Vamos calcular o título da mistura do instante (1). Como a mistura ocupa a panela de pressão inteira, e a massa da mistura é igual a massa inicial, podemos calcular o volume específico do instante (1):

O título será:

Utilizando o título, podemos calcular a energia interna para o instante 1:

Infelizmente não podemos calcular a energia interna do instante (2) tão facilmente. Mas podemos relacionar a energia interna e a massa ao título:

Relacionamos a massa ao volume específico:

E utilizando o volume específico, vamos relacionar a massa ao título:

Pronto, agora para relacionar a energia interna, primeiro temos que relacionar o volume específico do instante (2) com o título

A energia interna é dada por:

Vamos aplicar tudo no balanço de energia:

Vamos resolver cada parte separadamente:

Aplicando:

Reorganizando:

Pra finalizar a questão, basta calcular a massa do instante (2)