Um prédio de escritórios necessita de uma transferência de calor de 20 kW para manter sua temperatura interna em 21°C quando a temperatura externa é de 0°C. Uma bomba de calor por compressão de vapor com Refrigerante 134a como fluido de trabalho é utilizada para fornecer o aquecimento necessário. O compressor opera adiabaticamente com uma eficiência isentrópica de 82%. Especifique as pressões adequadas do evaporador e do condensador de um ciclo com esse propósito, admitindo que DTcond = DTevap = 10°C, conforme ilustrado na Fig. P10.37. Os estados estão numerados na Fig. 10.13. O refrigerante é vapor saturado na saída do evaporador e líquido saturado na saída do condensador nas respectivas pressões. Determine
(a) a vazão mássica de refrigerante, em kg/s.
(b) a potência do compressor, em kW.
(c) o coeficiente de desempenho e compare com o coeficiente de desempenho para um ciclo de bomba de calor de Carnot operando entre os reservatórios nas temperaturas interna e externa, respectivamente.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Desenhando o diagrama
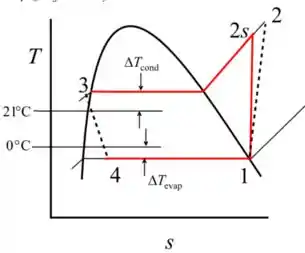
Passo 3
Calculando a temperatura no estado 3
Aqui, a diferença de temperaturas na entrada e saída do condensador é
Obtendo a pressão de saturação correspondente a da Tabela A-10 “Propriedades de Refrigerante 134a Saturado (Líquido Vapor): Tabela de Temperatura”, por interpolação
Passo 4
Calculando a temperatura no estado 1
Obtendo a pressão de saturação correspondente a da Tabela A-10 “Propriedades de Refrigerante 134a Saturado (Líquido Vapor): Tabela de Temperatura”, por interpolação
Passo 5
Obtendo as propriedades de vapor saturado de R134a a da Tabela A-11 “Propriedades de R134a Saturado (Líquido Vapor): Tabela de Pressão”, por interpolação
Calculando a pressão no estado 2
Já que 1-2 é um processo isentrópico
Passo 6
Obtendo a entalpia específica do R134a a pressão e da Tabela A-12 “Propriedades de R134a Saturado (Líquido Vapor): Tabela de Pressão”, por interpolação
Escrevendo a equação para a eficiência do compressor
Passo 7
a) Obtendo a entalpia específica do R134a a pressão da Tabela A-11 “Propriedades de R134a Saturado (Líquid Vapor): Tabela de Pressão”, por interpolação
Já que o processo 3-4 é de estrangulamento
Calculando a taxa de vazão mássica no condensador
Passo 8
b) calculando a potência de entrada do compressor
Passo 9
c) calculando o coeficiente de performance do ciclo
Passo 10
calculando o coeficiente de performance da bomba de calor de Carnot
Então, o coeficiente de performance do ciclo de Carnot é maior que o ciclo de Carnot do ciclo original.
Resposta
a)
b)
c) e