Enunciado
Termodinâmica - Introdução a termodinâmica da engenharia química, J.M.Smith Van Ness- Ed: 7º - Capítulo 5.Problemas - Ex. 1
Prove que é impossível o cruzamento de duas linhas representando processos adiabáticos reversíveis, em um diagrama PV. (Sugestão: Suponha que elas se cruzem, e se complete o ciclo com uma linha representando um processo isotérmico reversível. Mostre que a realização desse ciclo viola a segunda lei.
Passo 1
Considerando a sugestão apresentada pelo enunciado, o gráfico pode ser descrito conforme, onde indica a tempertura da fonte quente e representa a temperatura da fonte fria, e sendo a representação dos processos adibáticos reversíveis, no gráfico:
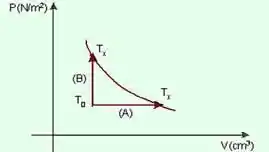
Passo 1
A segundao lei da termodinamica diz que a variação entropia total para um processo reversível é zero.
E também que a variação de entropia dentro de um processo ciclico também é zero, com isso a variação de entropia só depende da quantidade de calor da fonte.
Com isso nos processos a→b=c e b=c→d 
(variação de entropia é zero).
Passo 2
Considerando então que a entropia só vai depender do calor no processo d→a que é dado pela equação dos gases ideais ,
.
Com isso a entropia total do sistema é,
Chegando que a variação total de entropia em um processo cíclio é menor que zero.
Resposta
Esse resultado viola a segunda lei da termodinamica pois a variação de entropia total em um processo cíclico reversível é zero.