Reconsidere o Prob. 10-77. Usando o EES (ou outro programa), investigue o efeito da pressão de extração para a remoção de vapor da turbina, a fim de ser usado na unidade de processamento térmico e no aquecedor de água de alimentação aberto, sobre o fluxo de massa necessário. Trace uma curva para o fluxo de massa na caldeira como função da pressão de extração e discuta os resultados.
Passo 1
Tá legal! Então, do Prob. 10-77, vamos pegar o diagrama que ilustra o sistema:
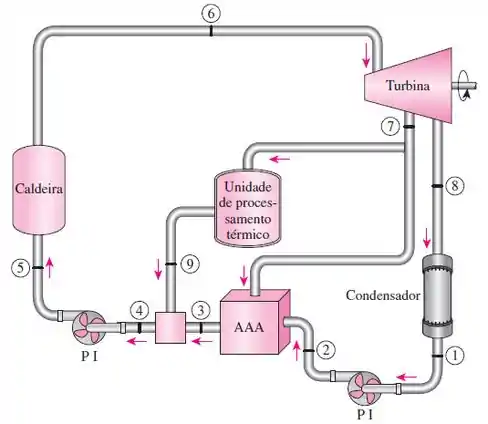
Agora, iremos utilizar o mesmo raciocínio empregado no exercício 10-77, só que agora o EES é quem vai fazer as contas para nós. Então, precisamos escrever as equações para cada componente, para a eficiência do sistema e descrever as pressões, temperaturas e títulos nos pontos de interesse para que o programa calcule as propriedades e consiga realizar todos os cálculos.
Passo 2
Dessa forma, o código em EES será:
"Dados fornecidos no Problema 10-77"
y = 0,35 "Fração mássica extraída para o reaquecedor de água"
P[6] = 9000 [kPa]
T[6] = 400 [C]
"P_extracao=1600 [kPa]"
P[7] = P_extracao
P_cond=10 [kPa]
P[8] = P_cond
W_dot_liq=25000 [kW]
Eta_turb= 100/100 "Eficiência isentrópica da turbina"
Eta_bomba = 100/100 "Eficiência isentrópica da bomba"
P[1] = P[8]
P[2]=P[7]
P[3]=P[7]
P[4] = P[7]
P[5]=P[6]
P[9] = P[7]
"Análise da bomba 1"
Fluid$='STEAM' "Fluido em estudo - vapor de água"
h[1]=enthalpy(Fluid$;P=P[1];x=0)
v1=volume(Fluid$;P=P[1];x=0)
s[1]=entropy(Fluid$;P=P[1];x=0)
T[1]=temperature(Fluid$;P=P[1];x=0)
w_bomba1_s=v1*(P[2]-P[1])
w_bomba1=w_bomba1_s/Eta_bomba "Definição da eficiência da bomba"
h[1]+w_bomba1= h[2]
s[2]=entropy(Fluid$;P=P[2];h=h[2])
T[2]=temperature(Fluid$;P=P[2];h=h[2])
"Análise do reaquecedor de água"
z*h[7] + (1- y)*h[2] = (1- y + z)*h[3]
h[3]=enthalpy(Fluid$;P=P[3];x=0)
T[3]=temperature(Fluid$;P=P[3];x=0)
s[3]=entropy(Fluid$;P=P[3];x=0)
"Anáise da unidade de processamento térmico"
(y - z)*h[7] = q_processo + (y - z)*h[9]
Q_dot_processo = m_dot*(y - z)*q_processo
h[9]=enthalpy(Fluid$;P=P[9];x=0)
T[9]=temperature(Fluid$;P=P[9];x=0)
s[9]=entropy(Fluid$;P=P[9];x=0)
"Análise da câmara de mistura"
(y-z)*h[9] + (1-y+z)*h[3] = 1*h[4]
T[4]=temperature(Fluid$;P=P[4];h=h[4])
s[4]=entropy(Fluid$;P=P[4];h=h[4])
"Análise da bomba 2"
v4=volume(Fluid$;P=P[4];x=0)
w_bomba2_s=v4*(P[5]-P[4])
w_bomba2=w_bomba2_s/Eta_bomba
h[4]+w_bomba2= h[5]
s[5]=entropy(Fluid$;P=P[5];h=h[5])
T[5]=temperature(Fluid$;P=P[5];h=h[5])
"Análise da caldeira"
q_e + h[5]=h[6]
h[6]=enthalpy(Fluid$;T=T[6];P=P[6])
s[6]=entropy(Fluid$;T=T[6];P=P[6])
"Análise da turbina"
ss[7]=s[6]
hs[7]=enthalpy(Fluid$;s=ss[7];P=P[7])
Ts[7]=temperature(Fluid$;s=ss[7];P=P[7])
h[7]=h[6]-Eta_turb*(h[6]-hs[7])
T[7]=temperature(Fluid$;P=P[7];h=h[7])
s[7]=entropy(Fluid$;P=P[7];h=h[7])
ss[8]=s[7]
hs[8]=enthalpy(Fluid$;s=ss[8];P=P[8])
Ts[8]=temperature(Fluid$;s=ss[8];P=P[8])
h[8]=h[7]-Eta_turb*(h[7]-hs[8])
T[8]=temperature(Fluid$;P=P[8];h=h[8])
s[8]=entropy(Fluid$;P=P[8];h=h[8])
h[6] =y*h[7] + (1- y)*h[8] + w_turb
"Análise do condensador"
(1- y)*h[8]=q_s+(1- y)*h[1]
"Análise do ciclo"
w_liq=w_turb - ((1- y)*w_bomba1+ w_bomba2)
Eta=w_liq/q_e
W_dot_liq = m_dot * w_liq
Passo 3
Com o código do passo 2, conseguimos os seguintes dados na tabela paramétrica para um intervalo de pressão de extração de:
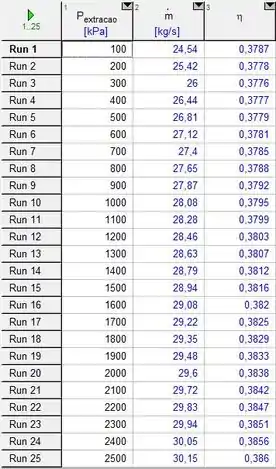
E, com esses valores, podemos plotar o gráfico da pressão de extração pela vazão mássica e da pressão de extração com relação a eficiência do sistema:
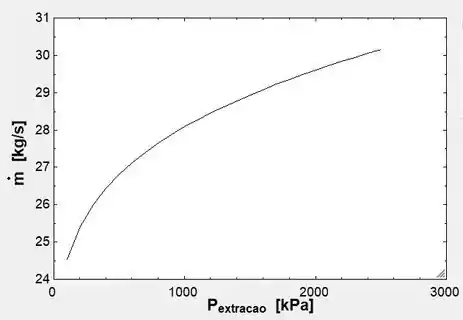
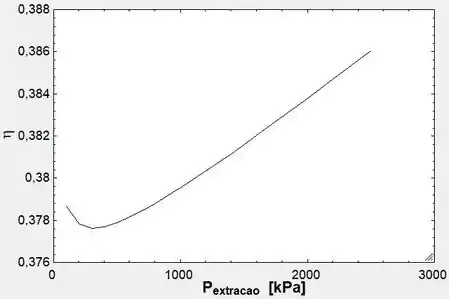
Com os dois gráficos, podemos ver que quanto maior a pressão de extração, maior a vazão mássica requerida pelo sistema e também maior será a eficiência do sistema como um todo.
Resposta
Ei, a resposta está no passo a passo :)