Reconsidere o Prob. 3–87. Resolva o problema usando o recurso do fator de compressibilidade do programa EES. Usando novamente o EES, compare o volume específico da água nos três casos a para a faixa de temperatura de a em intervalos de . Trace um gráfico do erro percentual da aproximação de gás ideal em função da temperatura e discuta os resultados.
Passo 1
UHUULL!!! Questões no EES! Este tipo de questão junta duas coisas bastante importantes dentro da engenharia: Termodinâmica e softwares que nos ajudam a modelar problemas. Sabendo disso, vamos pra cima! O problema anterior é considerado e vamos pegar um intervalo de até pulando de para a análise!
Passo 2
Dentro do nosso software, na parte de comandos, vamos definir nossas variáveis e então compilar gerando o gráfico! Temos:
P=15 [MPa]*Convert(MPa,kPa)
{T_Celsius= 350 [C]}
T=T_Celsius+273 “[K]”
T_critical=T_CRIT(Steam_iapws)
P_critical=P_CRIT(Steam_iapws)
{v=Vol/m}
P_table=P; P_comp=P;P_idealgas=P
T_table=T; T_comp=T; T_idelagas=T
v_table=volume(Steam_iapws,P=P_table,T=T_table) “dados do EES para o vapor como gas real”
{P_table=pressure(Steam_iapws, T=T_table,v=v)}
{T_sat=temperature(Steam_iapws,P=P_table,v=v)}
MM=MOLARMASS(water)
R_u=8.314 [kJ/kmol-K] “Constante universal dos gases”
R=R_u/MM “[kJ/kg-K] “[kJ/kg-K], constante dos gases particular”
P_idealgas*v_idelagas=R*T_idealgas “Equação de gás ideal”
z=COMPRESS(T_comp/T_critical, P_comp/P_critical)
P_comp*v_comp=z*R*T_comp “fator de compressibilidade generalizado”
Error_idealgas=Abs(v_table-v_idealgas)/v_table*Convert(,%)
Error_comp=Abs(v_table-v_comp)/v_table*Convert(, %)
Passo 3
Após executar o código, o compilador nos entrega uma tabela e um gráfico!
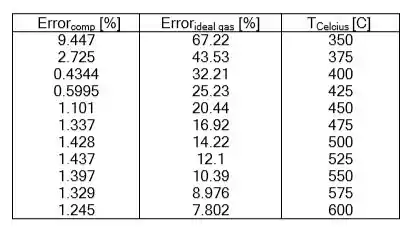
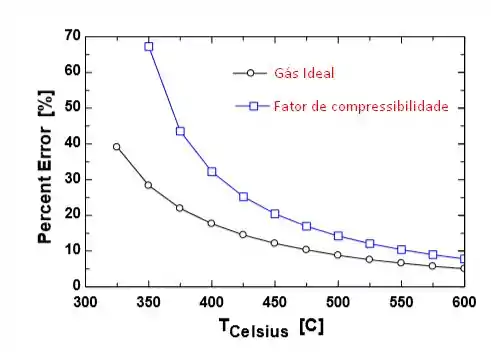
Resposta
Ei, a resposta está no passo a passo :)