Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 10.Problemas - Ex. 54
Reconsidere o Problema 10.53, mas inclua na análise o fato de tanto o compressor quanto a turbina terem eficiências isentrópicas de 84%. Responda às mesmas questões do Problema 10.53 para esse ciclo modificado e determine a taxa de produção de entropia no compressor e na turbina em Btu/min · °R.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?! Recomendo que você dê uma voltada na questão 53 pra relembrar o que a gente fez lá, beleza?
O que vai mudar da 53 pra essa é que a gente vai ter dois processos intermediários, devido a eficiência, 2s e 4s.
Passo 2
É dado que:
- Temperatura na entrada do compressor:
- Pressão na entrada do compressor:
- Pressão na saída do compressor:
- Temperatura na entrada do trocador de calor:
- Temperatura na entrada da turbina:
- Capacidade de refrigeração:
- Eficiência isentrópica do compressor:
- Eficiência isentrópica da turbina:
O diagrama é mostrado
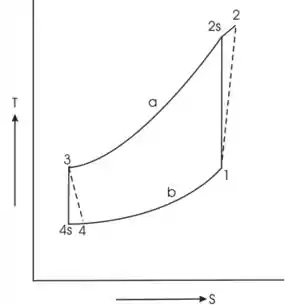
Passo 3
Da tabela de propriedades do ar a
O processo 1-2s é isentrópico, usando a relação isentrópica
Da tabela de propriedades do ar com , interpolando
Usando a eficiência isentrópica do compressor
Passo 4
Da tabela de propriedades do ar a
O processo 3-4 é isentrópico, usando a relação isentrópica
Da tabela de propriedades do ar com , interpolando
Usando a eficiência isentrópica da turbina
Da tabela de propriedades do ar com
Passo 5
Aplicando o balanço de energia na equação do trocador de calor
Sabemos que a capacidade de refrigeração é
Passo 6
a) usando a equação do gás ideal a taxa de razão volumétrica na entrada do compressor é
Passo 7
b) o coeficiente de performance é
Resposta
a)
b)