Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 70
Um refrigerador, com R-22 como fluido de trabalho, apresenta uma temperatura mínima de e uma pressão máxima de . Admita um ciclo de refrigeração ideal, conforme mostrado na Fig. 11.24. Determine as transferências de calor do espaço frio e para o espaço quente, ambas por unidade de massa, e o coeficiente de performance do refrigerador.
Passo 1
Fala, galera! Vamos resolver essa questão.
Vamos começar dando uma olhadinha no diagrama do ciclo:
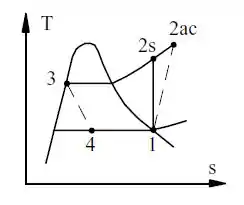
Por meio do diagrama, e do que foi apresentado no enunciado, temos que:
E
Com isso, conseguiremos obter os dados das propriedades na Tabela B.3. Então, vamos lá!
Passo 2
Primeiramente, vamos determinar cada uma das propriedades, estado por estado!
No estado 1, interno ao compressor, temos vapor de saturação de ,
No estado 2, de saída do compressor real, temos:
E para o estado 2s, de saída ideal:
No estado 3, na saída do condensador, temos a saturação do líquido a e
E finalmente, no estado 4, para a válvula de saída:
Com os dados estabelecidos, passaremos agora para a aplicação das equações.
Passo 3
Começamos pela equação de transferência de calor:
Agora para :
Calculando o trabalho real e ideal no compressor, temos:
E
Agora podemos determinar o coeficiente de desempenho do ciclo, fazendo:
E por fim:
E concluímos o exercício. Até a próxima, galera!