Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 69
Um refrigerador, usando R-22, é acionado por um pequeno motor térmico a gás natural com rendimento de , conforme mostrado na Fig. P11.69. O R-22 é condensado a e evaporado a , e o ciclo é o padrão de ar. Determine as duas transferências de calor por unidade de massa no ciclo de refrigeração. Qual é o coeficiente de performance global em termos da razão ?
Passo 1
Fala, galera! Vamos resolver essa questão.
Para esse problema precisaremos analisar a Tabela B.4.1 que representa as propriedades termodinâmicas do R-22. Além disso, precisaremos analisar o diagrama do ciclo de refrigeração:
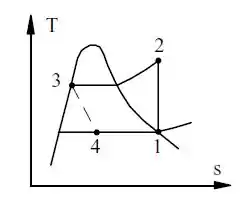
Por meio do diagrama, podemos determinar que a temperatura de condensação é a mesma do ponto 3 e a temperatura de evaporação é a mesma do ponto 1, ou seja:
Com isso, conseguiremos obter os dados necessários para calcular as duas transferências de calor e, em seguida, calcular o coeficiente de rendimento do ciclo e estabeleceremos a relação entre e . Então, vamos lá!
Passo 2
Primeiramente, vamos obter a transferência de calor do evaporador.
Como , então
Como , então
Com esses valores, conseguimos calcular a taxa de transferência de calor:
Agora vamos para o compressor!
Passo 3
Agora no compressor, temos no estado de entrada 1 e no estado de saída 2, cerca de e . Com isso, encontramos:
Calculando o trabalho no compressor, temos:
Agora podemos ir para o condensador!
Passo 4
Calculando a transferência de calor no condensador:
Agora podemos determinar o coeficiente de desempenho do ciclo, fazendo:
E por fim, vamos estabelecer a relação entre e através do cálculo do motor térmico:
E concluímos o exercício. Até a próxima, galera!