O Refrigerante 22 é o fluido de trabalho de um ciclo de refrigeração a vapor de Carnot para o qual a temperatura do evaporador é -30ºC. Vapor saturado entra no condensador a 36ºC e líquido saturado sai à mesma temperatura. A vazão mássica do refrigerante é 10 kg/min. Determine

(a) a taxa de transferência de calor para o refrigerante que escoa pelo evaporador, em kW.

(b) a potência líquida de acionamento do ciclo, em k\V.

(c) o coeficiente de desempenho.

Desenhando o diagrama para um ciclo de refrigeração de Carnot ideal

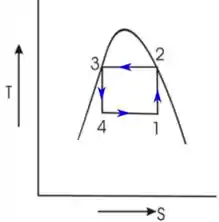
Aqui, temos que

• Processo 1-2: compressão isentrópica
• Processo 2-3: resfriamento isotérmico
• Processo 3-4: expansão isentrópica
• Processo 4-1: absorção de calor isotérmica

Determinando a taxa de transferência de calor para o refrigerante passando pelo evaporador

Aqui,

• é a vazão mássica
• é a entalpia específica no ponto 1
• é a entalpia específica no ponto 2

Achando as propriedades de vapor saturado do R-22 em da Tabela A-7 “Propriedades de Refrigerante 22 Saturado (Líquido-vapor): Tabela de Temperatura”

Achando as propriedades de vapor saturado do R-22 em da Tabela A-7 “Propriedades de Refrigerante 22 Saturado (Líquido-vapor): Tabela de Temperatura”

Identificando que o processo 1-2 é um processo isentrópico. Então

Resolvendo para o título

Determinando o valor da entalpia específica no ponto 1

Identificando que o processo 3-4 é um processo isentrópico. Então

Resolvendo para o título

Determinando o valor da entalpia específica no ponto 4

a) Substituindo valores na equação para a transferência de calor pelo evaporador

b) Calculando a potência de entrada para o ciclo

c) Calculando o coeficiente de performance do ciclo

d) Calculando a capacidade do refrigerante em toneladas