Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Yunus A. Çporel, Michael A. Boles - Termodinâmica- Ed: 5º - Capítulo 10.Problemas - Ex. 23

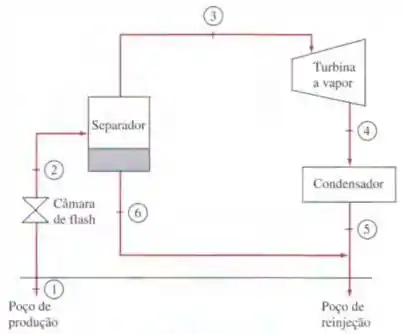
A representação esquemática de usina geotérmica de separador único é mostrada na figura P 10 - 23 . O líquido geotérmico está disponível como líquido saturado a 230 ° C . O líquido geotérmico é retirado do poço de produção a uma vazão de 230   k g / s , e é separado a uma pressão de 500   k P a por um processo de separação isoentálpico, no qual o vapor resultante é separado do líquido de um separador e encaminhado para a turbina. O vapor deixa a turbina a 10   k P a com conteúdo de umidade de 10 % e entra no condensador, onde é condensado e conduzido para um poço de rejeição juntamente com o líquido que sai do separador. Determine (a) o fluxo de massa do vapor na turbina, (b) a eficiência isoentrópica da turbina, (c) a potência produzida pela turbina e (d) a eficiência térmica da usina (a razão entre o trabalho produzido na turbina e a energia do fluido geotérmico em relação ás condições ambiente padrão).

Passo 1

Bora lá galera!

Assumindo que existem condições de operação estável e que as mudanças de energia cinética e potencial são desprezíveis.

Então temos que responder 4 alternativas, e por isso vamos começar buscando os dados das tabelas A-4, A-5 e A-6.

  1. T 1 = 230 ° C x 1 = 0   h 1 = 990,14   k J / k g

    P 4 = 500   k P a h 2 = h 1 = 990,14   k J / k g   x 2 = h 2 - h f h f g = 990,14 - 640,09 2108 = 0,1661

    A taxa de fluxo de massa de vapor através da turbina é:

    m ˙ 3 = x 2 ⋅ m ˙ 1 = 0,1661 ⋅ 230 = 38,20 k g s

    Uhull !! Primeira etapa concluída com sucesso!

    Passo 2

  2. Agora para a turbina, buscando os dados mais uma vez, temos que:

    3. P 3 = 500   k P a x 3 = 1   h 3 = 2748,1   k J / k g s 3 = 6,8207   k J / k g . K

    P 4 = 10   k P a s 4 = s 3   h 4 s = 2160,3   k J / k g

    P 4 = 10   k P a x 4 = 0,90   h 4 = h f + x 4 h f g = 191,81 + 0,90 ⋅ 2392,1 = 2344,7   k J / k g

    E, portanto, finalmente conseguimos calcular a eficiência isoentrópica da turbina:

    η T = h 3 - h 4 h 3 - h 4 s

    η T = 2748,1   - 2344,7     2748,1   - 2160,3

    η T = 0,686

    Passo 3

  3. A potência produzida pela turbina será:

    4. W ˙ T . o u t = m ˙ h 3 - h 4 = 38,20 ⋅ 2748,1 - 2344,7 = 15410   k W

    Passo 4

  4. Finalmente o último item dessa questão, em que nos pede para calcularmos a eficiência térmica da usina. Portanto:

T 0 = 25 ° C x 0 = 0   h 0 = 104,83   k J / k g

E ˙ i n = m ˙ 1 h 1 - h 0 = 230 ⋅ 990,14 - 104,83 = 203,622   k W

Até que enfim, calculamos a eficiência térmica da usina:

η t h = W ˙ T . o u t E ˙ i n

η t h = 15410 203,622   = 0,0757 = 7,6 %

Essa questão foi, heim... Bora pra próxima?

Resposta

  1. m ˙ 3 = 38,20 k g s
  2. η T = 0,686
  3. W ˙ T . o u t = 15410   k W
  4. η t h = 0,0757 = 7,6 %