Um sistema pistão-cilindro contém 1 kg de oxigênio conforme ilustrado na Fig. P3.115. Não há atrito entre os componentes do sistema mecânico e a pressão externa é 1 atm. O volume inicial é 1 m3 e a pressão no interior do cilindro 1 atm. Ocorre transferência de calor até que o volume seja o dobro do inicial. Determine a quantidade de calor transferido ao sistema, em kJ, assumindo k = 1,4 e ignorando efeitos de energia cinética e potencial.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
É dado que:
- Volume inicial no cilindro:
- Pressão inicial no cilindro:
- Volume final no cilindro:
- Razão de calor específico:
O esquemático do problema é o seguinte
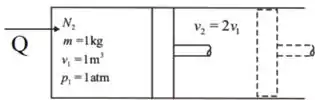
Passo 3
Pressão crítica para é
A pressão reduzida é dada por
Já que é bem pequeno
Então podemos usar a equação de gás ideal.
Passo 4
A pressão permanece constante durante o processo
A gente sabe que
Passo 5
Usando a primeira lei da termodinâmica, a transferência de calor para o processo é