Ar está submetido a um ciclo de refrigeração Ericsson, que é o reverso de um ciclo de potência Ericsson apresentado na Seção 9.8.4. A Fig. P10.58 fornece os dados para a operação do ciclo em regime permanente. Esboce o diagrama p–y para o ciclo e determine
(a) a transferência de calor para a expansão isotérmica, por unidade de massa de ar, em kJ/kg.
(b) o trabalho líquido por unidade de massa de ar, em kJ/kg.
(c) o coeficiente de desempenho.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama é mostrado abaixo
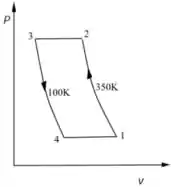
Passo 3
a) aplicando o balanço de energia para o ciclo
Aqui, é a entrada de calor no ciclo, é o trabalho produzido pela turbina
Já que a turbina trabalha em um processo de expansão isotérmica, então, a energia interna permanece constante
Passo 4
Calculando o trabalho da turbina usando a equação de expansão isotérmica
Aqui, é a constante dos gases para o ar, é a temperatura na entrada da turbina, é a pressão na entrada da turbina e é a pressão na saída da turbina
Passo 5
b) calculando o trabalho na entrada do compressor por unidade de massa
Aqui, é a constante dos gases para o ar, é a temperatura na entrada do compressor, é a pressão na entrada do compressor e é a pressão na saída do compressor
Calculando o trabalho líquido para o ciclo
Passo 6
c) calculando o coeficiente de performance do ciclo
Resposta
a)
b)
c)