A tabela a seguir fornece os dados de operação de um ciclo de refrigeração por compressão de vapor em regime permanente, com Refrigerante 134a como fluido de trabalho. Os estados estão numerados conforme a Fig. 10.3. A capacidade de refrigeração é de 4,6 TR. Ignorando os efeitos de transferência de calor entre o compressor e sua vizinhança, esboce o diagrama T–s para o ciclo e determine
(a) a vazão mássica do refrigerante, em kg/min.
(b) a eficiência isentrópica do compressor.
(c) o coeficiente de desempenho.
(d) as taxas de destruição de exergia no compressor e na válvula de expansão, ambas em kW.
(e) as variações líquidas da taxa de exergia de fluxo para o refrigerante que escoa, pelo evaporador e pelo condensador, respectivamente, ambas em kW. Admita T0 = 21°C, p0 = 1 bar.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama do ciclo de refrigeração de compressão de vapor é mostrado
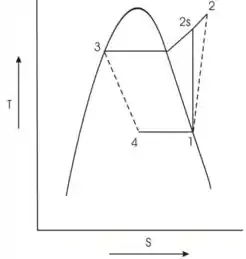
Passo 3
As propriedades no estado 1 são
A uma pressão de e . Das tabelas de vapor superaquecido por interpolação
Passo 4
a) a capacidade de refrigeração
Passo 5
b) a eficiência do compressor isentrópico
Passo 6
c) calculando o coeficiente de performance do sistema
Passo 7
d) calculando a taxa de destruição de exergia no compressor
calculando a taxa de destruição de exergia na válvula
Passo 8
e) o fluxo de exergia específica no evaporador
o fluxo de exergia específica no condensador
Resposta
a)
b)
c)
d) e
e) e