A tabela a seguir fornece os dados de operação de um ciclo de refrigeração por compressão de vapor em regime permanente, com propano como fluido de trabalho. Os estados estão numerados conforme a Fig. 10.3. A vazão mássica do refrigerante é de 8,42 lb/min (0,06 kg/s). A transferência de calor do compressor para sua vizinhança ocorre a uma taxa de 3,5 Btu por lb (8,1 kJ/kg) de refrigerante que passa pelo compressor. O condensador é resfriado a água que entra a 65°F (18,3°C) e sai a 80°F (26,7°C), com uma variação de pressão desprezível. Esboce o diagrama T–s para o ciclo e determine
(a) a capacidade frigorífica, em TR.
(b) a potência do compressor, em HP.
(c) a vazão mássica da água de resfriamento através do condensador, em lb/min.
(d) o coeficiente de desempenho.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Podemos considerar o seguinte diagrama
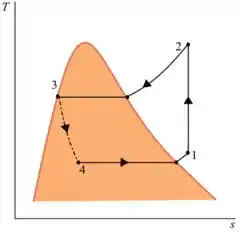
Passo 3
a) temos alguns dados importantes:
- Entalpia específica do propano no estado ponto 1:
- Entalpia específica do propano no estado ponto 2:
- Entalpia específica do propano no estado ponto 3:
- Entalpia específica do propano no estado ponto 4:
Escrevendo a expressão para a capacidade do refrigerante
Passo 4
b) Escrevendo a expressão para a potência do compressor
Passo 5
c) De acordo com a Tabela A-2E “Propriedades de Água Saturada (Líquido-Vapor): Tabela de Temperatura)” para obter a entalpia específica da água à
Calculando a entalpia específica da água à usando interpolação
Passo 6
Aplicando o balanço de energia para o condensador
Passo 7
d) escrevendo a expressão para o coeficiente de performance do ciclo
Resposta
a)
b)
c)
d)