Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 13.Problemas - Ex. 58
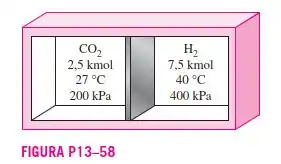
Um tanque rígido isolado é dividido em dois compartimentos por uma partição. Um compartimento contém de a e , e o outro compartimento contém de gás e . A partição é removida, e os dois gases se misturam. Determine a temperatura da mistura e a pressão da mistura após o estabelecimento do equilíbrio. Considere calores específicos constantes à temperatura ambiente para ambos os gases.
Passo 1
Letra a
Lembre-se de eventualmente ver as informações no final do livro!
Vamos usar:
Assim:
Então:
Passo 2
Letra b
Como:
Então:
Assim, para mistura:
Resposta
Letra a
Letra b
Exercícios de Livros Relacionados
Utilize as equações e a tabela de vapor para determinar as propriedades não apresentadas no conjunto ∅ ,weT B S . Admita que a pressão total é 100 kPa e verifique seus resultados com o diagrama psicro
Utilize o diagrama psicrométrico para determinar as propriedades não apresentadas no conjunto ∅ ,w ,T B SeT B U .a) ∅ = 5 0% ,w = 0,012 b) T B U = 1 5℃ ,∅ = 6 0% ℃ c) T B U = 17℃ ,w = 0,008 ℃ d) T B S
Determine as temperaturas de orvalho nos 4 estados indicados no Prob. 12.107.
Compare o ambiente em duas praias num dia nublado e com brisa. Na praia A , a temperatura é igual a 20° C , a pressão é 103,5k P a e a umidade relativa é 90 % . Na praia B , a temperatura é 25° C , a
Um trocador de calor, que opera a pressão constante e em regime permanente, é alimentado com ar a 100 kPa, 30° C e com umidade relativa de 40 % . Numa operação ele aquece este ar até 45° C e noutra op