Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 99

O tanque rígido A mostrado na Fig. P 3.99 , com volume interno de 1   m 3 , inicialmente contém ar a 1500   k P a e 300   K (que é a temperatura do ambiente onde está localizado o arranjo). A área da seção transversal do pistão do conjunto B indicado na figura é 0,1   m 2 e a pressão interna necessária para que ocorra o início do movimento do pistão é 250   k P a . A válvula é então aberta e o pistão muda de posição vagarosamente até que a distância entre o pistão e o fundo do cilindro seja igual a 2   m . Neste momento a válvula é fechada. Durante todo o processo a temperatura do ar permanece constante e igual a 300   K . Nestas condições, determine a pressão do ar no estado final do processo.

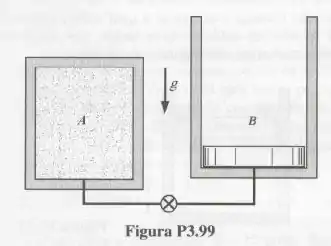
Passo 1

Temos um processo de temperatura constante.

Bem pessoal, nesta aqui estaremos calculando a massa contida no tanque A inicialmente A 1 .

E calcular quanto de massa foi transferido para o tanque B 2 , B não possui inicial porque inicialmente B está vazio.

Sabendo quanto de massa o tanque A transferiu para o tanque B , A 1 - B 2 = A 2 , poderemos calcular a pressão final no tanque A .

Mas com qual fórmula vamos fazer isso tudo?

Utilizaremos a fórmula do gás real:

P V = m R T

Apenas ela isso mesmo hahahha, partiu?

Passo 2

Calculando a massa A 1 :

Temos que as variáveis iniciais são:

P A 1 = 1500   k P a

T A = 300   K

V A =   1   m 3

Olhando na tabela A . 1.5 encontramos o R do ar, que é:

R = 0,287 k J k g ∙ K

Substituindo tudo na fórmula, temos:

m A 1 = P A 1 V A   R T A = 1500 ∙ 1 0,287 ∙ 300 = 17,422   k g

Passo 3

Vamos calcular a massa que transferiu para o tanque B .

Basicamente utilizaremos mesma fórmula.

Apenas o volume que será:

V B = A ∙ h = 0,1 ∙ 2

E a pressão será a pressão necessária para elevar o pistão.

P B = 250   k P a

Aplicando a fórmula:

m B = P B ∙ V B R T B = 250 ∙ 0,1 ∙ 2 0,287 ∙ 300 = 0,581   k g

Passo 4

Temos que a massa final no tanque A é?

m A 2 = m A 1 - m B = 17,422 - 0,581 = 16,841   k g

Aplicando a fórmula agora pra determinar a pressão, temos:

P V = m R T

P = m R T V

P A 2 = 16,841 ∙ 0,287 ∙ 300 1 = 1450   k P a

Resposta

P A 2 = 1450   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um quilograma de R-134a preenche 0,090m 3 de um recipiente rígido a uma temperatura inicial de - 40° C . O recipiente é então aquecido até que a pressão seja de 280k P a . Determine a pressão inicial
59. Um arranjo pistão-cilindro contém 0,8 kg de vapor de água a 300 °C e 1 MPa. O vapor é resfriado a pressão constante até que metade da massa condense.(a) Mostre o processo em um diagrama T-v.(b) En
64. 100 gramas de R-134a inicialmente preenchem a metade de um dispositivo pistão-cilindro a 60 kPa e -20 °C. O dispositivo é então aquecido até a temperatura de 100 °C. Determine a alteração no volum
68. Um tanque rígido de 0,3 m3 contém inicialmente uma mistura saturada de líquido e vapor de água a 150 °C. Em seguida, a água é aquecida até atingir o estado crítico. Determine a massa da água líqui
60. Um tanque rígido contém vapor de água a 250 °C a uma pressão desconhecida. Quando o tanque for resfriado a 124 °C, o vapor começará a condensar. Estime a pressão inicial do tanque.