Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 14.Problemas - Ex. 73

Ar úmido saturado a 200   k P a e 15   ° C e aquecido ate 30   ° C à medida que escoa por um tubo de 4   c m de diametro a uma velocidade de 20   m / s . Desprezando as perdas de pressão, calcule a umidade relativa na saída do tubo e a taxa de transferência de calor (em k W ), para o ar.

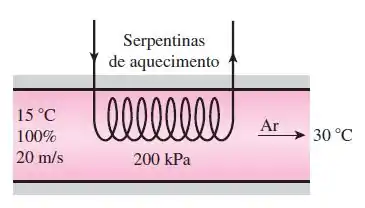
Passo 1

Temos nossas condições de entrada e temos que determinar a taxa de calor de aquecimento.

Precisamos determinar a umidade relativa de saída.

Assumindo que o processo está em regime permanente. Portanto, o fluxo de massa é equivalente na entrada e saída ( m ˙ i n = m ˙ o u t ).

Ar seco e água são gases ideais.

A variação da energia cinética e potencial é insignificante.

A quantidade de umidade permanece igual durante o processo, ou seja, ( ω 1 = ω 2 ). Utilizando as condições de entrada vamos determinar as propriedades de entrada olhando no diagrama psicrométrico (Figura A-31).

Determinando as propriedades, para assim determinar h 1 e h 2 para utilizar a equação do balanço de energia para determinar a taxa:

P v 1 = ϕ 1 P g 1 = ϕ 1 ∙ P g 1 - 15 ° C = 1 ∙ 1,7057   k = 1,7057   k P a

h g 1 = h g - 15 ° C = 2528,3   k J / k g

P a 1 = P 1 - P v 1 = 200 - 1,7057 = 198,29   k P a

Utilizando a formula do gás ideal podemos determina o volume específico de entrada:

v 1 = R a T 1 P a 1

v 1 = 0,287 ∙ 288 198,29 k

v 1 = 0,4168 m 3 k g   d e   a r   s e c o

Utilizando a formula de umidade relativa temos:

ω 1 = 0,622 ∙ P v 1 P 1 - P v 1  

ω 1 = 0,622 ∙ 1,7057   k 200 - 1,7057   k

ω 1 = 0,005350   k g   H 2 O k g   d e   a r   s e c o = ω 2

Agora que temos todas a propriedades de entrada, podemos determinar h 1 :

h 1 = c p ∙ T 1 + ω 1 ∙ h g 1

h 1 = 1,005 ∙ 15 + 0,00535 ∙ 2528,3

h 1 = 28,60 k J k g   d e   a r   s e c o

Passo 2

Utilizando os mesmos itens utilizados para determinar as propriedades de entrada utilizaremos para as de saída:

P v 2 = P v 1 = 1,7057   k P a

P g 2 = P s a t - 30 ° C = 4,2469   k P a

Com isto temos a umidade relativa de saída do ar:

ϕ 2 = P v 2 P g 2

ϕ 2 = 1,7057 k 4,2469 k

ϕ 2 = 0,402 = 40,2 %

Continuando na busca para determinar h 2 :

h g 2 = h g - 30 ° C = 2555,6   k J / k g

ω 1 = ω 2

Finalmente podemos calcula-lo:

h 2 = c p T 2 + ω 2 h g 2

h 2 = 1,005 ∙ 20 + 0,005350 ∙ 2555,6

h 2 = 43,82 k J k g   d e   a r   s e c o

Passo 3

Encontramos h 1 , h 2 e para completar nossa equação do balanço de energia temos que encontra o fluxo de massa.

Para isso iremos calcular primeiro o fluxo volumétrico para ai sim utilizar a formula de fluxo de massa:

V ˙ = V 1 A 1 = π D 2 V 1 4 = 20 ∙ π ∙ 0,04 2 4

V ˙ = 0,02513   m 3 / s

Calculando o fluxo de massa:

m ˙ = V ˙ v 1

m ˙ = 0,02513 0,4168 = 0,06029   k g / s

Passo 4

E finalmente podemos calculara taxa de calor de aquecimento:

Q ˙ = m ˙ ∙ h 2 - h 1

Q ˙ = 0,06029 ∙ 43,82 - 28,60

Q ˙ = 0,918   k W

Resposta

Umidade relativa de saída do ar: ϕ 2 = 0,402 = 40,2 %

Taxa de calor de aquecimento:

Q ˙ = 0,918   k W

Ver Outros Exercícios desse livro