Usando a Eq. 5.13, responda aos seguintes itens que envolvem ciclos reversíveis e irreversíveis:
a) Um ciclo de potência reversível e outro irreversível rejeitam cada um a energia para um reservatório frio à temperatura e recebem a energia de reservatórios quentes nas temperaturas e respectivamente. Não ocorrem outras trocas de calor. Mostre que .
b) Um ciclo de refrigeração reversível e outro irreversível rejeitam cada um à energia para um reservatório quente à temperatura e recebem a energia de reservatórios quentes nas temperaturas é , respectivamente. Não ocorrem outras trocas de calor. Mostre que .
c) Um ciclo de uma bomba de calor reversível e outro irreversível recebem cada um a energia de um reservatório frio à temperatura e rejeitam a energia para reservatórios quentes nas temperaturas e , respectivamente. Não ocorrem outras trocas de calor. Mostre que .
Passo 1
Antes de mais nada, uma questão completinha pra você não esquecer mais como fazer e nem como são dadas as relações em ciclos de potência, ciclos de refrigeração e bombas de calor.
Como não seria diferente, o Responde Aí preparou essa resolução, especialmente pra você, com muito amor e carinho pra guardar no coração.

Antes de mais nada, vale mostrar o seguinte:
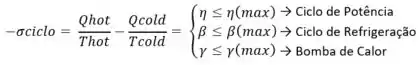
Com isso, podemos somente separar as alternativas por passos. Partiu?
Passo 2
a) Ciclo de Potência e com “Mostre que ”
Simples, podemos colocar como comparação a relação de eficiência e, com isso, a Desigualdade de Clausius já se mostra presente. Ou seja:
E, aqui, como , e são mantidos iguais, APENAS COMO CRITÉRIO COMPARATIVO, podemos considerar:
O que gera:
Passo 3
b) Ciclo de Refrigeração e com “Mostre que ”
Vamos lembrar que a relação de refrigeração está INVERTIDA de acordo com o processo de comparação entre transmissão de calor e diferença de temperatura pois:
Logo, de acordo com a Desigualdade da eq 5.13, é possível, APENAS COMO CRITÉRIO COMPARATIVO, considerar que:
Passo 4
c) Bomba de Calor e com “Mostre que ”
No caso da bomba, é preciso um pouco mais de visão além do alcance. Mas não tema, pois pegamos o Olho de Tandera emprestado e te entregamos essa visão.

Sendo
Podemos juntar esse algebrismo aqui ó:
Para criar a Visão do Olho de Tandera, ou seja:
Só que o problema menciona mesmos reservatórios e mesmas transferências de e . Ou seja, APENAS COMO CRITÉRIO COMPARATIVO, é possível considerar que:
Com isso, temos:
Resposta
a) → →
b) → →
c) → →