Usando o enunciado de Kelvin-Planck da segunda lei da termodinâmica, demonstre os seguintes corolários:

(a) O coeficiente de desempenho de um ciclo de refrigeração irreversível é sempre menor do que o coeficiente de desempenho de um ciclo de refrigeração reversível quando ambos trocam energia por transferência de calor com os mesmos dois reservatórios.

(b)Todos os ciclos de refrigeração reversíveis que operam entre os mesmos dois reservatórios têm o mesmo coeficiente de desempenho.

(c) O coeficiente de desempenho de um ciclo de bomba de calor irreversível é sempre menor do que o coeficiente de desempenho de um ciclo de bomba de calor reversível quando ambos trocam energia por transferência de calor com os mesmos dois reservatórios.

(d) Todos os ciclos de bomba de calor reversíveis que operam entre os mesmos dois reservatórios têm o mesmo coeficiente de desempenho.

Podemos desenhar o ciclo assim

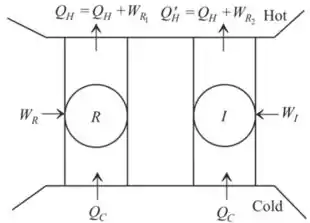
Podemos ver que é reversível e é o ciclo de refrigeração irreversível. Cada ciclo remove uma quantidade de energia do reservatório frio.

a) Considerando que opera na direção oposta com , e tendo as mesmas magnitudes. Nesse caminho, o sistema combinado opera no ciclo trocando energia com uma reserva única, por exemplo um reservatório quente. Então

Aqui, incluímos a inequação, por conta do ciclo irreversível está incluído. Então

Já que cada ciclo recebe a mesma quantidade de energia, , então

b) Considerando o mesmo esquemático, só que agora é e agora é outro ciclo reversível .

Considerando também que opera em duas direções opostas. Então o sistema combinado troca energia com um reservatório simples, por exemplo um reservatório quente. Então

Ambos os ciclos recebem entrada de energia cada

c) Desenhando o ciclo

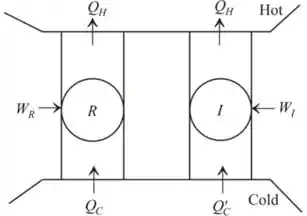
Podemos ver que é o ciclo de bomba reversível e é o ciclo de bomba irreversível.

Considerando a direção de varia com , e tendo a mesma magnitude.

O sistema combinado opera trocando energia com um reservatório único, por exemplo o reservatório quente. Então, usando o enunciado de Plank

Já que cada ciclo rejeita a mesma quantidade de energia, , então

d) Considerando o esquemático do Passo 5, só que agora é e é . Temos que opera na direção oposta. Então o sistema combinado agora troca energia com um reservatório simples, por exemplo um reservatório simples. Então

Ambos os ciclos rejeitam calor cada. Então