Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 47
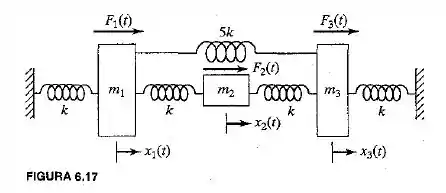
Use equações de Lagrange para deduzir as equações de movimento de cada um dos sistemas mostrados nas Figuras 6.17 a 6.21.
Passo 1
Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?
Inicialmente, se localizem na figura 6.21, a quinta a ser considerada.
Da fórmula da energia cinética, nós encontramos o seguinte:
Da energia potencial, nós temos:
Sabendo que .
Passo 2
Dito isso, já podemos, assim como nas questões anteriores, montar as equações para a primeira coordenada:
Para a segunda coordenada:
Para a terceira coordenada:
Para a quarta coordenada:
Passo 3
Finalmente podemos montar as equações de movimento a partir das equações de Lagrange: