Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 8.Problemas - Ex. 27
Vapor a e entra na turbina do primeiro estágio de um ciclo ideal de Rankine com reaquecimento. O vapor que deixa de reaquecimento do gerador de vapor está a , e a pressão no condensado é de . Se o título na saída da turbina do segundo estágio é de , determine a eficiência térmica do ciclo.
Passo 1
E aí, galerinha! Oia nós aqui de novo!
Bom! Temos aí um exercício sobre sistemas de vapor e turbinas, especialmente, turbinas!
E como essa parte é meio complicada, vamo começar fazendo um esboço do nosso problema com os dados que temos do enunciado...
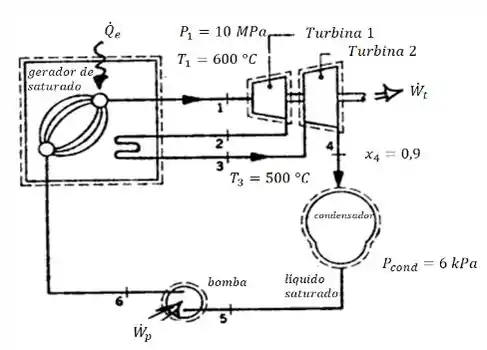
Assim, baseado nessa figura podemos construir o seguinte gráfico do ciclo de temperatura :
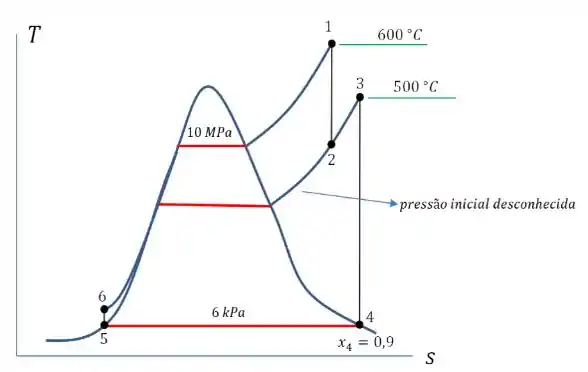
Pronto! Já temos mais ou menos quase tudo no esquema!
Passo 2
Agora, com base em tabelas como a do livro, mostrada abaixo...
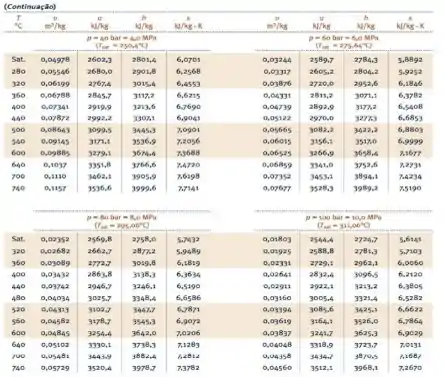
Vamos encontrar as condições referentes aos principais estados destacados na figura do final do !
Para o estado onde , ; temos que:
Para o estado onde , ; temos que:
Passo 3
Para o estado , onde como podemos ver e , temos um problema. Não dá pra obter o valor exato apenas olhando pra tabela abaixo...
É por isso que preciso recorrer à interpolação! Dando uma olhada nas tabelas da parte , podemos ver que , tá localizado numa zona de pressão entre e .
Dessa forma, usando interpolação...
E então, fazendo o mesmo pra entalpia...
Passo 4
Para o estado , com e , por sua vez, temos que...
E quase acabando aqui... Para o estado , como temos apenas líquido à ...
Pronto! Aí tá de boas! Como já temos os dados que precisamos... Pra achar , basta usar a fórmula abaixo, já que o título não muda...
Da tabela , à , temos que...
Dessa forma, obtemos que...
Passo 5
Que beleza! A parte mais complicadinha já foi! Agora, vamos tratar de achar a eficiência!
Analisando o ciclo na figura do , temos que o trabalho do ciclo dividido pela vazão mássica fica assim...
Isso como podemos ver, pode ser reescrito como...
O que nada mais é do que escrever em termos das entalpias que temos!
Quanto à quantidade de energia na entrada, ela pode ser escrita também como...
Aí sim! Pra achar a eficiência então, basta dividir essa segunda pela primeira... Ou seja, a quantidade de entrada pelo trabalho...
Substituindo os valores numéricos...
Achamos nossa resposta! Eureeeeeeeeca!