Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 134

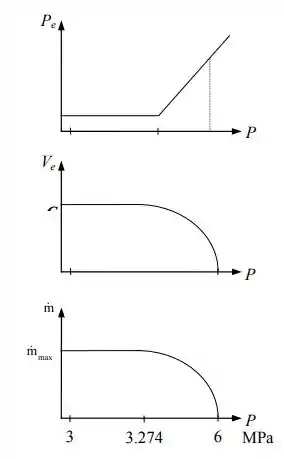
Vapor de água a 6,0   M P a   e 700   K entra em um bocal convergente a uma velocidade desprezível. A área de garganta do bocal é de 8   c m 2 . Considerando um escoamento isentrópico, esboce graficamente a pressão de saída, a velocidade de saída e a vazão mássica através do bocal versus a contrapressão P c p para 6,0 ≥ P c p ≥ 3,0   M p a . Considere o vapor de um gás ideal com k = 1,3 , c p = 1,872   k J / ( k g ∙ K ) e R = 0,462   k J / ( k g ∙ K )

Passo 1

Fala aí galera, vamos para mais um problema de Termodinâmica. As propriedades do fluido no local onde M a = 1 são as propriedades críticas. Primeiro, vamos determinar a temperatura e a pressão de estagnação, que permanecem constantes em todo o bico, uma vez que o fluxo é isentrópico.. Fica assim:

T 0 = T i T 0 = 7 00   K

E também:

P 0 = P i P 0 = 6   M p a

Com isso, a velocidade :

T * = T 0 2 k + 1 = 500   K 2 1,667 + 1 T * = 375   K

Quanto à pressão, temos: P * = P 0 2 k + 1 k k + 1 = 6   M P a 2 1,3 + 1 1,3 1,3 - 1 P * = 3,274   M P a

Então, para a pressão no plano de saída, temos:

P e = P b           para P b ≥ 3,274   M P a P e = P * = 3,274   M P a           para P b < 3,274   M P a

Passo 2

Para determinar a temperatura, temos:

T e = T 0 P e P 0 k - 1 k T e = 700   K P e 6 0,3 / 1,3

E para a velocidade:

V = 2 c p T 0 - T e = 2 1,872 k J k g ∙ K 700 - T e 1000   m 2 / s 2 1   k J / k g  

Susbtituindo na densidade, temos:

ρ e = P e R T e = P e ( 0,462   k P a ∙ m 3 / k g ∙ K T e

Quanto à massa, temos:

m = ρ e V e A e = ρ e V e ( 0,0008   m 2 )

Com isso, nossos gráficos da pressão de saída, da velocidade de saída e da vazão mássica ficam, respectivamente, assim:

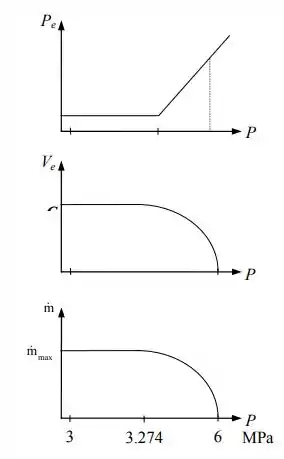
Resposta

Ver Outros Exercícios desse livro