Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 49
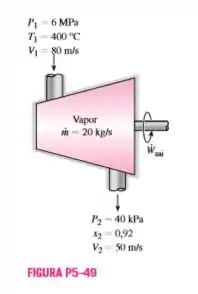
Vapor escoa em regime permanente por uma turbina adiabática. Na entrada, o vapor está a 6 Mpa, 400 °C e 80 m/s, e na saída, a 40 kPa, 92% de título e 50 m/s. O fluxo de massa do vapor é de 20 kg/s. Determine (a) a variação da energia cinética, (b) a potência produzida e (c) a área de entrada da turbina.
Passo 1
Em (a) queremos descobrir a variação da energia cinética na turbina, assim:
Passo 2
Temos que o balanço de energia é dado por:
Adotando a turbina como sistema, temos:
- A turbina opera em regime permanente, ;
- A turbina é adiabática, ;
- A variação de altura nas correntes é desprezível, ;
Assim, o balanço de energia da turbina fica da seguinte forma:
Passo 3
Analisando as condições de entrada na turbina, conseguimos identificar nas tabelas de vapor que a entalpia específica do vapor na entrada é de e seu volume específico é de .
Já na saída da turbina, como não temos somente vapor, teremos que a entalpia específica será dada por:
Pela tabela, encontramos que e que , assim, temos:
Substituindo no balanço de energia, teremos que a potência produzida pela turbina é de:
O sinal negativo representa que este trabalho está sendo gerado, ou seja, sai da turbina.
Passo 4
Temos que o fluxo mássico é dado por:
Substituindo os valores na expressão, temos:
Resposta
Assim,
- -1,95 kJ/kg;
- -14,6 kW;
- 0,0119 .