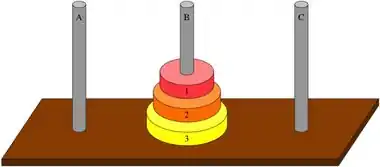
Elabore um algoritmo que mova três discos de uma Torre de Hanói, que consiste em três hastes (a – b – c), uma das quais serve de suporte para três discos de tamanhos diferentes (1 – 2 – 3), os menores sobre os maiores. Pode-se mover um disco de cada vez para qualquer haste, contanto que nunca seja colocado um disco maior sobre um menor.
O objetivo é transferir os três discos para outra haste.
Passo 1
Em primeiro lugar, nós devemos decidir para que haste iremos transferir os três discos. Nesse exemplo, transferiremos da haste B para a haste A.
Vale lembrar que o menor número de movimentações possíveis para transferir todos os discos de uma determinada haste para outra é dado por:
Onde é o número de discos da torre.
Sendo assim, nesse exemplo o menor número possível de movimentos é:
Resposta
A lógica da torre de Hanói é utilizar uma das hastes como auxiliar para que um disco maior nunca fique sobre um menor. Dessa forma, o algoritmo para movimentar os discos da haste B para a haste A é:
