Repita o Exercício 3 usando a regra do ponto médio e os resultados do Exercício 9.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Vamos lá, considerando , a regra do ponto médio para aproximar uma integral é dada por
Vamos calcular as integrais entre e , usando os valores aproximados obtidos no exercício 9 e o erro usando a regra do ponto médio.
A – Tendo como . A integral será igual a
E o valor encontrado no exercício é igual a
Portanto, o erro é igual a
O erro para a regra do ponto médio é dada por , onde . Desde que
A magnitude do erro será igual a
Portanto,
O que significa que a regra do ponto médio e o valor de erro são consistentes com o resultado
Passo 2
B – A função . A integral tem como resultado
O valor aproximado é dado por
Portanto, o erro entre a integral e a aproximação é igual a
O erro para a regra do ponto médio é dado por onde . A fim de encontrar um limite para o erro para a regra do ponto médio, calculamos a segunda derivada de f como segue
Utilizando um software para plotar a segunda derivada, demonstrando que ela é negativa e decrescente
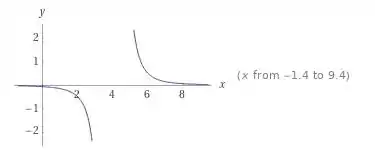
Então, a magnitude do erro é no máximo
Portanto,
O que indica que a regra do ponto médio e o limite de erro são consistentes com o resultado.
Passo 3
C – Tendo como função , com , a integral atual entre a e b é igual a
Com isso, nós temos que
E o valor aproximado
Logo, o erro será igual a
Já sabemos como funciona o erro para a regra do ponto médio, então já podemos partir para o cálculo da primeira e segunda derivadas
E
Pela configuração, já sabemos que a segunda derivada é positiva e crescente. Logo, a magnitude do erro é dada por
Portanto,
Resultados consistentes 😊.
Passo 4
D – Pegando como função , com , a integral nesse caso é igual a
E o valor aproximado é
E com isso, o erro entre os dois casos é igual a
Calculando a primeira e segunda derivadas, nós obtemos o seguinte resultado
E
O módulo para a segunda derivada no intervalo de . Portanto
A magnitude do erro é
Portanto, os resultados são consistentes
Passo 5
E – Tendo como função , com . Logo, a integral é igual a
E o valor aproximado
E o erro
Resposta
Resposta nos passos