Sistemas Lineares e Não Lineares

Fala aí! Seja muito bem vindo ao Responde Aí, a plataforma de exatas que vai salvar o seu semestre!

Vem comigo que hoje vamos começar a falar sobre sistemas lineares e não lineares.

Você pode não lembrar, mas já cansou de ver e resolver sistemas lineares no ensino médio.

É SÉRIO. Dá uma olhada nesse probleminha aqui:

"Joãozinho observou que haviam 15 veículos estacionados em sua rua, dentre eles motos e carros. Ao se abaixar no chão, ele conseguiu contar 48 rodas. Qual a quantidade de motos e de carros estacionados na rua de Joãozinho?"

Esse é um problema que resolvíamos muito no ensino médio e talvez até no fudamental. O que fazíamos era definir varíaveis, montar duas equações e resolvê-las. Assim:

Equações:

E depois resolvíamos de maneira bem simples substituindo uma equação na outra.

Era bem tranquilo não é?

Mas o problema é que agora que estamos na faculdade o nível aumentou um pouco... Agora podemos ter sistemas como esse, mas ao invés de duas equações podemos ter muitas, de 5 pra cima....

Por isso é importante a gente desenvolver outros métodos para resolver esses sistemas.

Uma coisa que ajuda muito é escrever o sistema linear na forma matricial.

Vamos pegar o exemplo de sistema que vimos lá no início:

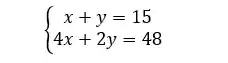
Para reescrevê-lo na forma matricial, vamos seguir essa equação aqui:

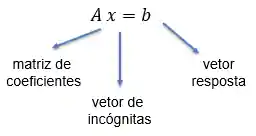
No nosso exemplo, o vetor de incógnitas será esse aqui:

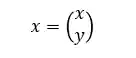
Desse modo, a matriz de coeficiente será:

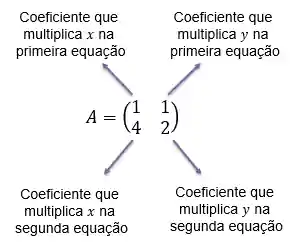
e o vetor de resposta esse:

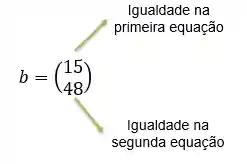
A partir dessa representação do sistema conseguimos aplicar diversos métodos de resolução que facilitam, e muito, a nossa vida!

Tá, beleza. Mas e os sistemas não lineares?

Os sistemas não lineares são aqueles que as equações não envolvem somente soma e subtração, mas também tem expoentes, frações, raíz quadrada, etc.

Resolver esses sistemas é um pouco mais complicadinho, mas nada que você precise se desesperar. O que vamos fazer é linearizar esse sistema, de forma a torná-lo linear, e aplicar os métodos para sistema linear, ou aprender um método específico para a resolução deles.

Quer comerçar a aprender esses métodos para resolução de sistemas de maneira rápida, descontraída, com linguagem amigável e ainda ter acesso a muitos exercícios resolvidos passo a passo?

Então confere o nosso Raio-X aqui, veja tudo que temos para te oferecer sobre sistemas lineares e não lineares e não se arrependa de fechar com a gente!