Cálculo de Autovalores

Fala aí, vamos aprender como calcular autovalores com métodos numéricos?

Primeiro, vamos entender o que é um autovalor. Dizemos que um escalar é um autovalor de uma matriz quadrada, , se existe um vetor , diferente de zero, tal que:

Em outras palavras, menos complicadas hahaha, se temos uma matriz quadrada , multiplicamos ela por um vetor e temos como resultado o próprio vetor multiplicado por um escalar , então dizemos que esse escalar é autovalor da matriz . Sacou?

Beleza, sabemos o que é um autovalor, mas como calculamos os autovalores de uma matriz?

Digamos que temos essa matriz aqui:

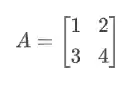
Lá em álgebra linear, a gente aprende a calcular esses autovalores de forma analítica mesmo. A gente acha um polinômio de dado por:

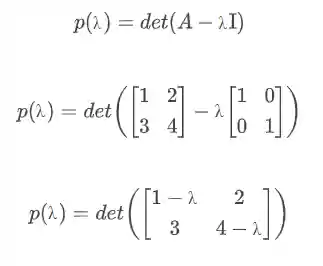
E calculamos as raízes desse polinômio. Essas raízes são os autovalores da matriz.

Parece tranquilo né?

Quando temos matrizes pequenas, como no exemplo que vimos, é tranquilo mesmo, mas imagina que temos uma matriz muuuuuuiiito grande?

Ferrou? Não mesmo... É aí que entram os métodos de cálculo de autovalores.

Esses métodos são métodos numéricos, ou seja, não vamos resolver analiticamente e achar exatamente os autovalores, mas vamos achar valores muito próximos do valor real.

O método mais conhecido é o método das potências.

Método das Potências

O método das potências é uma técnica iterativa e é usada para determinar o autovalor dominante, ou seja, o autovalor de maior módulo.

Através do método das potências encontramos não só o autovalor de maior módulo, mas também o autovetor associado a ele.

Aprenda sobre esse método assitindo a esse vídeo aqui 👇🏽, feito pela equipe incrível do Responde Aí:

Além desse método há também mais dois métodos: Método de Francis e Método de Householder.

Quer aprender sobre esses métodos de cálculo de autovalor? Então confere aqui em seguida o nosso Raio-X, onde todo o conteúdo incrível que nós preparamos para você está organizado pensando no melhor para o seu estudo. 👇🏽 😉