Suponha uma barra de metal homogêneo, como na figura a seguir, onde .

A temperatura ao longo de é mantida constante e igual a , enquanto que ao longo de ela é igual a . A distribuição do calor na barra obedece à seguinte equação:

Com as condições de contorno:

A solução numérica desse problema pode ser obtida considerando-se uma divisão do retângulo em retângulos menores a partir de uma divisão de em intervalos iguais de amplitude e de uma divisão de em intervalos iguais de amplitude , como é mostrado na figura a seguir:

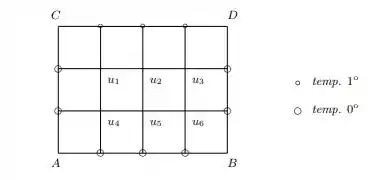
Nessa figura estamos considerando . A temperatura u nos pontos internos pode ser obtida numericamente simulando as derivadas segundas de , pelas diferen¸cas de segunda ordem de modo que para , obtemos:

para cada par em R. Assim, por exemplo, para o ponto da figura anterior vale:

Considerando todos os pontos da figura anterior obtemos um sistema de 6 equações lineares nas incógnitas: . Resolva-o por método numérico à sua escolha, com garantia de convergência.

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide Suponha uma barra de metal homogêneo, como na figura a seguir, onde .

A temperatura ao longo de é mantida constante e igual a , enquanto que ao longo de ela é igual a . A distribuição do calor na barra obedece à seguinte equação:

Com as condições de contorno:

A solução numérica desse problema pode ser obtida considerando-se uma divisão do retângulo em retângulos menores a partir de uma divisão de em intervalos iguais de amplitude e de uma divisão de em intervalos iguais de amplitude , como é mostrado na figura a seguir:

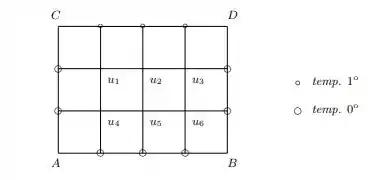
Nessa figura estamos considerando . A temperatura u nos pontos internos pode ser obtida numericamente simulando as derivadas segundas de , pelas diferen¸cas de segunda ordem de modo que para , obtemos:

para cada par em R. Assim, por exemplo, para o ponto da figura anterior vale:

Considerando todos os pontos da figura anterior obtemos um sistema de 6 equações lineares nas incógnitas: . Resolva-o por método numérico à sua escolha, com garantia de convergência.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.