Numa treliça estaticamente determinada com juntas articuladas, como dada na figura a seguir:
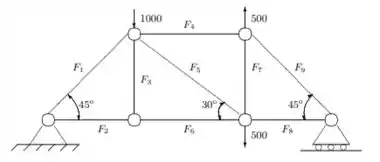
a tensão, , em cada componente pode ser obtida da seguinte equação matricial:

Observe que as equações são obtidas fazendo-se a soma de todas as forças horizontais ou verticais em cada junta igual a zero. Além disso a matriz dos coeficientes é bastante esparsa, e assim um candidato natural é o método de Gauss-Seidel.
a) As equações podem ser rearranjadas de modo a se obter uma matriz estritamente diagonalmente dominante?
b) E o sistema convergente se iniciarmos com um vetor com todas as componentes iguais a zero?
c) Resolva o sistema pelo método de Gauss-Seidel, partindo do vetor nulo e obtendo a solução com precisão de .
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide uma treliça estaticamente determinada com juntas articuladas, como dada na figura a seguir:
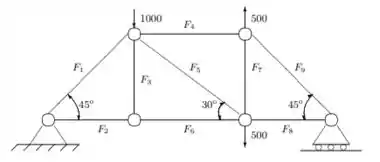
a tensão, , em cada componente pode ser obtida da seguinte equação matricial:

Observe que as equações são obtidas fazendo-se a soma de todas as forças horizontais ou verticais em cada junta igual a zero. Além disso a matriz dos coeficientes é bastante esparsa, e assim um candidato natural é o método de Gauss-Seidel.
a) As equações podem ser rearranjadas de modo a se obter uma matriz estritamente diagonalmente dominante?
b) E o sistema convergente se iniciarmos com um vetor com todas as componentes iguais a zero?
c) Resolva o sistema pelo método de Gauss-Seidel, partindo do vetor nulo e obtendo a solução com precisão de .

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha na letra (a) para determinarmos quantas equações podem ser rearranjadas de modo a se obter uma matriz estritamente diagonal temos,
Já na letra (b) a resposta é sim pois se iniciarmos todas a componentes com zero seu sistema tende a ser convergente ficando maior que zero.
E na letra partindo do vetor nulo temos,
Temos sistema igual a zero com valor mínimo igual a
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b) sim pois se iniciarmos todas a componentes com zero seu sistema tende a ser convergente ficando maior que zero.
c) a zero com valor mínimo igual a