15. Suponha que entre dois ambientes e haja troca de calor. Sejam e as temperaturas no instante, nos ambientes e , respectivamente. Admita que as temperaturas estejam variando nas seguintes taxas
Suponha que e . (As temperaturas são dadas em graus centígrados e o tempo em segundos)
A- Mostre que as temperaturas estão variando periodicamente com tempo.
B - Determine e .
C - Determine as temperaturas máxima e mínima no ambiente .
D - Determine a trajetória descrita pelo ponto .
Passo 1
Poxa! As soluções vão variar periodicamente se elas envolverem seno e cosseno. Para isso acontecer, os autovalores da matriz de coeficientes devem ser imaginários! Matematicamente falando, aqui está a Matriz de coeficientes:
Os Autovalores dela são encontrados assim:
Bem, como é apenas subtrair da diagonal principal...
Resolvendo o determinante...
Ora, (o número imaginário) então...
Ou seja, de fato estamos lidando com autovalores complexos, logo a solução será periódica!
Passo 2
A solução de um sistema de EDO com imaginário é:
Onde e são:
Ora, e vem do autovalor complexo:
No nosso caso:
Portanto...
Já e vem do autovetor complexo ( é a parte real e o imaginário). Vamos então determinar esse autovetor !
Passo 3
Os autovetores podem ser calculados assim:
Então para o teremos de coordenadas desconhecidas complexas :
Ora, sabemos que asta subtrair da diagonal:
Essas duas linhas são Linearmente dependentes e sempre serão! Então, basta pegar a primeira linha e multiplicar com a coluna e igualar a (produto de matrizes):
Se falarmos que , então...
Então um autovetor para é:
Lembre-se que você pode pegar outro valor para , desde que seja está valendo!
Aqui não precisa encontrar para o autovalor , pois só com o , já podemos falar quem é e quem é . Rescrevendo o vetor em parte real e imaginária...
Então...
Passo 4
Com isso podemos retornar para os valores de e ...
E substituir:
Então a solução será...
Juntando tudo vamos obter o seguinte...
Para determinar e , podemos usar o fato de que e :
Então...
Passo 5
Ora, a temperatura vai ser máxima no ponto onde sua derivada for nula, lembra? (basicamente estamos encontrando os pontos críticos)
Derivando então...
Jogando esse seno para o outro lado...
Quem é então? ISSO! onde é um número inteiro! Ou seja, para Então...
E para
E o valor de maior temperatura será:
O de menor temperatura será...
Passo 6
Poxa! Aqui temos uma questão de Retrato de fase! Afinal, queremos desenhar a trajetória de !
Sabemos que quando o é imaginário, com o , as trajetórias serão elipses centrada na origem:
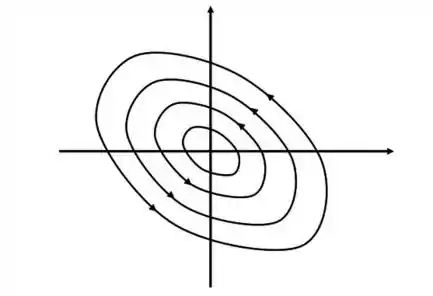
No nosso caso, teremos uma única elipse, pois sabemos que o é particular!
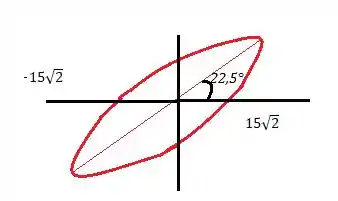
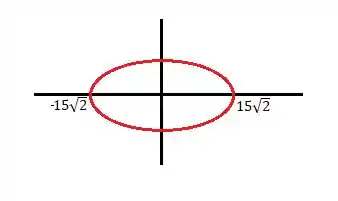
Ele tem um valor máximo de temperatura e um mínimo de , o que sugere que a nossa elipse tem um eixo maior de :
Além disso, a nossa elipse tem esse eixo maior para quando , ou quando :
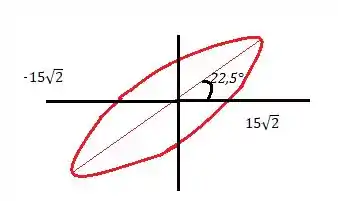
Resposta
Letra A: Autovalores complexos.
Letra B:
Letra C: Temperatura Máxima é e mínima de .
Letra D: