Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 65
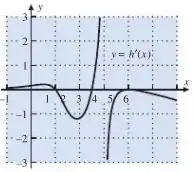
65. A figura em anexo mostra o gráfico da derivada de uma função que está definida e é contínua no intervalo . Suponha que o gráfico de tenha uma assíntota vertical em e que:
a) Quais são os pontos críticos de ?
b) Identifique os intervalos em que é crescente.
c) Identifique as coordenadas dos extremos relativos de e classifique-os como máximo ou mínimo relativos.
d) Dê uma estimativa das coordenadas dos pontos de inflexão de .
Passo 1
a) Então galera, a dificuldade dessa questão é que devemos imaginar um gráfico tendo informações de , logo, precisamos relembrar do significado da derivada primeira no gráfico de uma função. Quando a derivada é então ela é dita crescente, e quando a derivada é ela é dita decrescente. Os pontos críticos da nossa função serão os pontos no qual no gráfico que nos foi dado, uma vez que é o gráfico da derivada.
Observando o gráfico com cuidado podemos observar que isso acontece nos pontos:
Como a função não está definida em , então esse valor também é um ponto crítico.
Passo 2
b) Nossa função será crescente quando , certo? Sendo assim, os intervalos que isso ocorre será nas partes em que a curva está acima do eixo , ou seja, em positivo. Se observarmos o gráfico, notaremos que isso ocorre em:
Além de:
Fora desses intervalos a função é negativa, ou seja, decrescente.
Passo 3
c) Para encontrarmos os pontos de extremos relativos, dado um gráfico de , temos que analisar o sinal da derivada nos pontos críticos, galera! Os pontos críticos foram descobertos no passo , certo? Então vamos utiliza-los!
Para temos que:
Se a derivada estava crescendo e começou a decrescer, então é ponto de máximo.
Para temos que:
Se a derivada estava decrescendo e começou a crescer, então é ponto de mínimo.
Para a função não muda de sinal, então não podemos concluir nada sobre isso, assim como não podemos dizer nada sobre .
Passo 4
d) Então pessoal, os pontos de inflexão em um gráfico de derivada são os pontos de pico (máximo ou mínimo) da derivada. Vale ressaltar que alguns pontos são leves e sutis, a ponto de as vezes não conseguirmos perceber, mas isso não vai acontecer nesse gráfico, então let’s go!
Observando o gráfico com cuidado podemos observar que há um pequeno pico em . Também há um pico em aproximadamente e, por fim, há um pico em . Logo, nossos possíveis pontos de inflexão estão em:
E está aí nossa resolução, pessoal!
Resposta
a)
b)
c) é ponto de máximo e é ponto de mínimo.
d)