Exercícios de Esboço de Gráfico - Lista de Exercícios Resolvida
Questão 1
Considere
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Utilizando as informações obtidas abaixo nos itens anteriores, faça um esboço do gráfico de .
Ver solução completaQuestão 2
Considere a função:
Cujas derivadas primeira e segunda são, respectivamente:
- O domínio da função;
- As assíntotas horizontais e verticais, caso existam;
- Os intervalos onde a função é crescente e decrescente;
- Os valores máximo e mínimo locais e/ou globais caso existam;
- Os intervalos onde a concavidade é para cima, onde é para baixo e os pontos de inflexão;
- Utilizando as informações adquiridas esboce um gráfico de .
Questão 3
Considere a função:
Cujas derivadas primeira e segunda são, respectivamente:
- O domínio da função;
- As assíntotas horizontais e verticais, caso existam;
- Os intervalos onde a função é crescente e decrescente;
- Os valores máximo e mínimo locais e/ou globais caso existam;
- Os intervalos onde a concavidade é para cima, onde é para baixo e os pontos de inflexão;
- Utilizando as informações adquiridas esboce um gráfico de .
Questão 4
Considere a função . Determine:
O domínio de ;
Os interceptos;
As simetrias de ;
As assíntotas;
Intervalos de crescimento e decrescimento;
Valores máximos e mínimos locais;
Discuta concavidade e dê os pontos de inflexão;
Use a informação obtida para esboçar o gráfico de .
Ver solução completaQuestão 5
Considere a função:
E as suas primeira e segunda derivadas.
a) Ache as assíntotas horizontais e verticais caso existam.
b) Identifique os intervalos onde a função é crescente e onde é decrescente.
c) Encontre os valores máximo e mínimo locais e/ou globais caso existam.
d) Identifique os intervalos de concavidade para cima e para baixo e os pontos de inflexão.
e) Usando as informações anteriores faça um esboço do gráfico de .
Ver solução completaQuestão 6
Considere a função dada por
- Encontre, caso existam, as assíntotas verticais e horizontais ao gráfico de .
- Determine os pontos críticos de , intervalos onde a função é crescente e onde a função é decrescente.
- Encontre os extremos relativos e absolutos de , caso existam.
- Determine os intervalos onde o gráfico da função possui concavidade voltada para cima e concavidade voltada para baixo.
- Esboce o gráfico da função .
Questão 7
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 8
Seja a função dada por:
- Determine, caso existam, as equações das assíntotas horizontais do gráfico de
- Determine, caso existam, os intervalos onde é crescente
- Esboce o gráfico de . Marque em seu desenho as assíntotas horizontais e as abscissas dos pontos de máximo local e de mínimo local do gráfico de , caso existam.
- O gráfico de tem ponto de inflexão? Justique sua resposta.
Questão 10
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 11
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 12
4. Esboce o gráfico da função , indicando:
- Interseções com os eixos coordenados;
- Regiões de crescimento e decrescimento, máximos e mínimos locais;
- Regiões de concavidade para baixo e para cima e pontos de inflexão;
- Comportamento no infinito e assíntotas;
- Máximo e mínimo absoluto.
Questão 13
Esboce o gráfico de , determinando o seu domínio, os intervalos de crescimento e decrescimento, a concavidade e calculando todos os limites necessários.
Ver solução completaQuestão 14
Esboce o gráfico de , determinando o seu domínio, os intervalos de crescimento e de decrescimento, concavidades e assíntotas (caso existam).
Ver solução completaQuestão 15
Considere
- é contínua em ? é derivável em ?
- Calcule e
- Determine os pontos críticos de .
- Em quais intervalos é crescente?
- Em quais intervalos é decrescente
- Determine, se houver, os pontos de mínimo local de .
- Determine, se houver, os pontos de máximo local de .
- Em quais intervalos, se houver, o gráfico de é côncavo para cima?
- Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
- Determine, se houver, os pontos de inflexão do gráfico de .
- Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Questão 17
Considere :
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Esboce o gráfico da função.
Ver solução completaQuestão 18
Considere uma função contínua . Com as seguintes propriedades
- é crescente nos intervalos e
- é decrescente nos intervalos e
Responda as questões abaixo
- Esboce o gráfico da função
- Quanto vale ? Quanto vale ?
- Qual o número mínimo de soluções da equação ?
Questão 19
Considere :
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Utilizando as informações obtidas abaixo nos itens anteriores, faça um esboço do gráfico de .
Ver solução completaQuestão 20
Considere definida por
- Determine os pontos críticos de .
- Em quais intervalos é crescente?
- Em quais intervalos é decrescente
- Determine, se houver, os pontos de mínimo local de .
- Determine, se houver, os pontos de máximo local de .
- Em quais intervalos, se houver, o gráfico de é côncavo para cima?
- Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
- Determine, se houver, os pontos de inflexão do gráfico de .
- Calcule e
- Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Questão 21
Seja :
Determine os intervalos de crescimento e de decrescimento de ;
Determine os pontos de máximos e mínimos locais de ;
O gráfico da função é.
Ver solução completaQuestão 22
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 23
Considere a função . Determine:
O domínio de ;
Os interceptos;
As simetrias de ;
As assíntotas;
Intervalos de crescimento e decrescimento;
Valores máximos e mínimos locais;
Discuta concavidade e dê os pontos de inflexão;
Use a informação obtida para esboçar o gráfico de .
Ver solução completaQuestão 24
Considere a função:
Cujas derivadas primeira e segunda são, respectivamente:
- O domínio da função;
- As assíntotas horizontais e verticais, caso existam;
- Os intervalos onde a função é crescente e decrescente;
- Os valores máximo e mínimo locais e/ou globais caso existam;
- Os intervalos onde a concavidade é para cima, onde é para baixo e os pontos de inflexão;
- Utilizando as informações adquiridas esboce um gráfico de .
Questão 25
Considere a função , definida para e
- Calcule
- Determine, se existirem:
- As assíntotas verticais e horizontais de ;
- Os intervalos onde é crescente e onde é decrescente;
- Os pontos de máximo e mínimo locais e/ou globais (abscissa e ordenada);
- Os intervalos onde tem concavidade para cima (convexa), concavidade para baixo (côncava) e os pontos de inflexão de ;
- Faça um esboço do gráfico de
Questão 26
Esboce o gráfico da função
determinando domínio, interceptos, a existência de assíntotas verticais e horizontais, intervalos de crescimento e decrescimento, pontos extremos, concavidade e pontos de ineflexão.
Ver solução completaQuestão 27
Considere a seguinte função
Encontre o domínio de , os pontos de interseção do gráfico de com os eixos e analise a simetria de .
Caso existam, determine as assíntotas horizontais e verticais de .
Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo e os seus valores.
Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de usando as informações obtidas nos itens anteriores.
Ver solução completaQuestão 28
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 29
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 30
Considere a função dada por
- Determine os intervalos onde é crescente e onde é decrescente. Determine os pontos de máximo e de mínimo locais de .
- Determine os intervalos onde possui concavidade para cima e também onde possui concavidade para baixo. Determine os pontos de inflexão de .
- Calcule os limites pertinentes a existência de assíntotas.
- Esboce o gráfico de
Questão 31
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 33
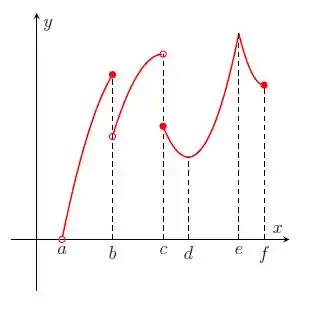
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
Questão 34
Considere a função dada por:
Determine:
Os intervalos onde é crescente, onde é decrescente e os máximos e mínimos locais, caso existam;
Os intervalos onde o gráfico de é côncavo para cima, onde é côncavo para baixo, e as abscissas dos pontos de inflexão, caso existam;
Os extremos absolutos, caso existam.
Ver solução completaQuestão 35
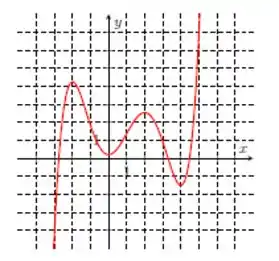
Nos itens abaixo, dado o gráfico da função , determine as concavidades e os pontos de inflexão. Caso algum ponto necessário não esteja explicitamente marcado na figura, dê um nome a esse ponto e escreva sua resposta utilizando-o.
Questão 36
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 37
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 38
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 39
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 40
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 41
Considere a função:
(i) Encontre o domínio de .
(ii) Caso existam, determine as assíntotas horizontais e verticais de .
(iii) Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo locais e globais e os seus valores.
(iv) Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
(v) Encontre os pontos de interseção do gráfico de com os eixos e esboce o gráfico de usando as informações obtidas nos itens anteriores.
Ver solução completaQuestão 42
3) repita o que foi feita no feito no exercício acima para as funções seguintes;
c)
Ver solução completaQuestão 43
Um modelo para a concentração no instate de uma droga injetada na corrente sanguínea é
Onde são constantes positivas e . Esboce o gráfico da função concentração. O que o gráfico nos diz sobre como a concentração varia conforme o tempo passa?
Ver solução completaQuestão 45
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 46
Considere a função .
- Determine o domínio de e os pontos de Interseção do gráfico com os eixos coordenados.
- Caso existam, determine as assíntotas horizontais e verticais.
- Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo e os seus valores.
- Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
- Esboce o gráfico de usando as informações obtidas nos itens anteriores.
Questão 47
4) Seja a função dada por:
- Determine o domínio da função
- Determine as equações das retas assíntotas horizontais do gráfico de , caso existam.
- Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
- Determine o(s) intervalo(s) de crescimento e de decrescimento de .
- Determine o(s) intervalo(s) onde o gráfico de f tem concavidade voltada para cima e onde tem concavidade voltada para baixo
- Esboce o gráfico de e suas retas assíntotas horizontais e verticais, caso existam
Questão 49
Seja uma função contínua em . Suponha que o gráfico da derivada seja dado pela figura abaixo:
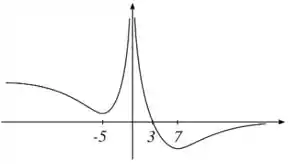
Considere as seguintes afirmações sobre o gráfico de :
é necessariamente um ponto de mínimo local.
é necessariamente um ponto de máximo local.
é necessariamente o valor máximo absoluto.
é necessariamente um ponto de inflexão.
Selecione a alternativa correta:
As afirmações e são verdadeiras e e são falsas
Todas as afirmações são falsas
As afirmações e são verdadeiras e e são falsas
Todas as afirmações são verdadeiras
As afirmações e são verdadeiras e e são falsas
Ver solução completaQuestão 50
Seja uma função derivável até segunda ordem. O gráfico de sua derivada está ilustrado abaixo. Assinale a afirmação FALSA
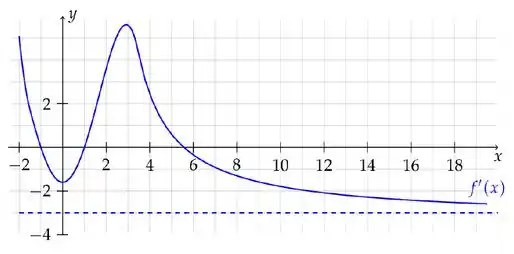
a) tem um único ponto de mínimo local, que ocorrem em
b) A equação tem pelo menos duas soluções reais distintas.
c) em
d) Pode ocorrer de a equação ter exatamente uma solução real.
e) tem mínimo global.
Ver solução completaQuestão 51
Seja .
Determine o domínio de e os intervalos de crescimento e decrescimento de .
Verifique que . Determine e estude a concavidade de .
Calcule os limites necessários e esboce o gráfico de .
Ver solução completaQuestão 52
Seja :
Calcule , , e ;
Verifique que e determine os intervalos de crescimento e decrescimento de ;
Estude a concavidade de ;
Pesquise a existência de assíntotas em e ; esboce o gráfico de .
Ver solução completaQuestão 53
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 54
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 55
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 56
5. Esboce o gráfico da função , destacando todos os passos utilizados.
Ver solução completaQuestão 57
Seja
Determine o domínio de
Determine os intervalos de crescimento e os intervalos de decrescimento de
Determine os pontos de máximo e de mínimo de
Determine todas as assíntotas da curva
Esboce o gráfico de contemplando tudo que foi calculado acima
Ver solução completaQuestão 58
- Seja a função , determine:
- Esboce o gráfico da função e determine a sua imagem.
Ver solução completaQuestão 59
Seja \ uma função com segunda derivada contínua e tal que:
- Determine . Qual o número de raízes que a função possui?
- Esboce, destacando todos os pontos relevantes, o gráfico de .
Questão 60
Considere uma função tal que as suas três primeiras derivadas são contínuas e . Além disso, satisfaz as seguintes propriedades:
e não se anula fora de ;
.
O que se pode concluir a respeito da concavidade do gráfico de à direita e à esquerda de ? Faça um esboço de um gráfico compatível com essas informações. Justifique a sua resposta.
Ver solução completaQuestão 61
Determine os intervalos de crescimento e de decrescimento e esboce o gráfico (calcule para isto todos os limites necessários).
Ver solução completaQuestão 62
Considere a função
- Determine as assíntotas horizontais e verticais caso existam.
- Determine os intervalos de crescimento e decrescimento, bem como os pontos críticos. Encontre e classifique os extremos relativos de .
- Determine os intervalos de concavidade voltada para cima e para baixo, indicando os pontos de inflexão.
- Esboce o gráfico da função, destacando os elementos encontrados nos itens anteriores.
Questão 63
Considere a função .
- Determine os intervalos de crescimento e decrescimento, bem como os pontos críticos. Encontre os pontos de máximo e mínimo locais de .
- Determine os intervalos de concavidade voltada para cima e para baixo, indicando os pontos de inflexão, caso existam.
- Determine as assíntotas horizontais e verticais, caso existam.
- Esboce o gráfico da função, destacando os elementos encontrados nos itens anteriores.
Questão 64
A figura abaixo representa o gráfico de uma função .
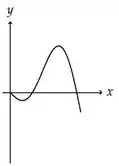
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 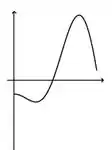
b) 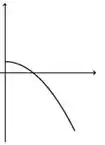
c) 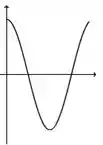
d) 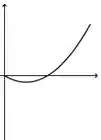
e) 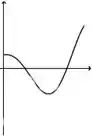
Questão 65
A figura abaixo representa o gráfico de uma função .
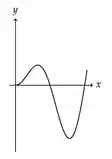
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 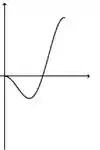
b) 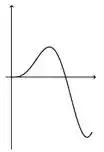
c) 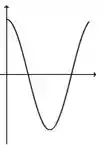
d) 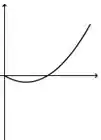
e) 
Questão 66
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 67
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 68
Seja
- Encontre as assíntotas horizontais e verticais, caso existam, da função .
- Determine os intervalos onde a função é crescente ou decrescente. Encontre também os pontos de máximo e mínimo locais e absolutos da função, assim como os respectivos valores da função nesses pontos.
- Determine os intervalos onde a função é côncava para cima ou para baixo, assim como os seus pontos de inflexão.
- Use as informações dos itens (a)-(c) para esboçar o gráfico de .
Questão 69
Considere a função dada por
- Encontre, caso existam, as assíntotas verticais de .
- Determine os pontos críticos de , intervalos onde a função é crescente e onde a função é decrescente.
- Encontre os extremos relativos e absolutos de , caso existam.
- Mostre que é côncava para cima.
- Esboce o gráfico de .
Questão 70
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 71
Considere a função dada por:
- Determine, caso exista(m):
(a.1) O(s) intervalo(s) de crescimento e decrescimento de .
(a.2) O(s) ponto(s) de máximo local e de mínimo local de .
(a.3) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
(a.4) O(s) ponto(s) de inflexão do gráfico de .
b) Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão determinado(s) nos itens anteriores. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão.
Passo 1
(a.1) Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de . Então vamos começar derivando a função:
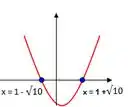
Assim:
Intervalo de crescimento de :
Intervalo de decrescimento de :
Passo 2
(a.2) Vamos achar os pontos críticos para podermos determinar os máximos e mínimos locais, se existirem.
A próxima etapa é fazer o Teste da Primeira ou da Segunda derivada. Nesse caso, já que temos o gráfico do item anterior pra ajudar, vamos fazer o Teste da Primeira Derivada, ou seja, analisar o sinal da derivada perto dos pontos críticos. Olha só:
- Em a derivada muda de positiva para negativa, logo esse é um ponto de máximo local
- Em o sinal da derivada não muda, logo não é nem máximo nem mínimo local
- Em a derivada muda de negativa para positiva, logo esse é um ponto de mínimo local
Questão 72
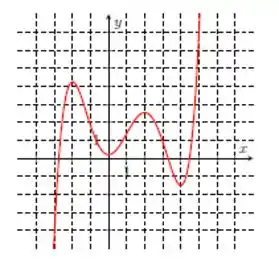
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
Questão 73
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
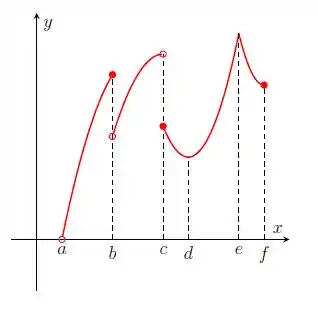
Questão 74
Considere a curva:
Esboce o gráfico da curva determinando, caso existam: Assíntotas horizontais e verticais, intervalos de crescimento e decrescimento, pontos críticos, extremos relativos (locais), concavidades e pontos de inflexão.
Ver solução completaQuestão 76
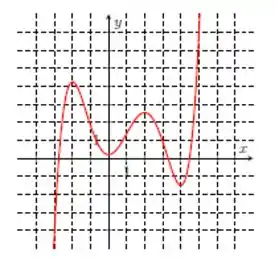
Nos itens abaixo, dado o gráfico da função , determine as concavidades e os pontos de inflexão. Caso algum ponto necessário não esteja explicitamente marcado na figura, dê um nome a esse ponto e escreva sua resposta utilizando-o.
Questão 77
Considere a função com derivadas e dadas por:
- Dê o domínio de definição de .
- Determine as assíntotas horizontais e verticais, caso existam.
- Identifique os pontos críticos, os extremos relativos e os intervalos onde a função é crescente e onde é decrescente.
- Encontre os pontos de inflexão de , se houver, e os intervalos de concavidade para cima e para baixo.
- Usando as informações anteriores, faça um esboço do gráfico de .
Questão 78
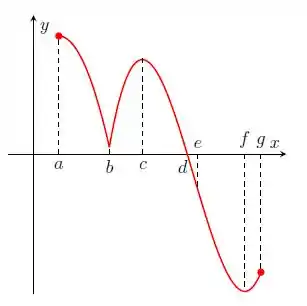
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
Questão 79
Para a função dada por:
a) Determine os intervalos de crescimento e decrescimento.
b)Faça o estudo da concavidade.
c) Determine as assíntotas horizontais.
b) Esboce o gráfico.
Ver solução completaQuestão 80
Considere a função definida por
a) Determine o domínio da função .
b) Determine os intervalos de crescimento e os de decrescimento de , caso existam.
c) Determine as equações das retas assíntotas horizontais e verticais do gráfico de , caso existam.
d) Utilizando as informações obtidas nos itens anteriores, esboce o gráfico de e suas retas assíntotas, caso existam.
Ver solução completaQuestão 81
Para a função
Determine os pontos críticos, pontos de inflexão, intervalos de crescimento e decrescimento e o estudo da concavidade.
Ver solução completaQuestão 82
Escreva a equação da reta tangente às curvas no ponto especificado. Esboce o gráfico de e da reta tangente.
Questão 83
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 84
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 87
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 88
Questão 3:
Seja a função dada por
- Determine o domínio da função .
- Determine o(s) intervalo(s) onde é decrescente.
- Determine as equações das retas assíntotas horizontais e verticais do gráfico de , caso existam.
- Utilizando as informações obtidas nos itens anteriores, esboce o gráfico de e suas retas assíntotas, caso existam.
Questão 89
Considere a função dada por:
- Determine, caso exista(m), o(s) intervalo(s) de crescimento e decrescimento de .
- Determine, caso exista(m), o(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
- Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão.
Questão 90
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 91
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 92
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 93
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 94
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 95
Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Questão 96
Seja a função dada por:
- Encontre os intervalos e tais que é inversível para todo , é inversível para todo e
- Para cada intervalo obtido no item anterior, faça um esboço em um mesmo plano cartesiano da reta com os gráficos das funções e
- Determine o domínio, a imagem e a expressão da função inversa de tal que o gráfico de passe pelo ponto
Questão 98
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 100
Seja
- Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo/minimo
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão
- Caso existam, encontre as assíntotas horizontais e verticais
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens , e
Questão 101
1) Seja dada por
Esboce o gráfico de localizando intervalos de crescimento e decrescimento, concavidades, limites convenientes e assíntotas (quando existirem). Use que:
Ver solução completaQuestão 102
3) Considere a função
Determine, caso existam:
- O domínio da função
- As equações das assíntotas verticais do gráfico de
- As equações das assíntotas horizontais do gráfico de
- Os intervalos de crescimento e decrescimento de
- Os intervalos onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
- Utilizando as informações obtidas nos itens anteriores, esboce o gráfico da função . Marque em seu desenho as assíntotas verticais e horizontais e as abscissas dos pontos de máximo local, mínimo local e de inflexão do gráfico de , caso existam.
Questão 103
4) Considere a função , sendo suas derivadas primeira e segunda dadas, respectivamente, por e . Siga o roteiro abaixo para esboçar um gráfico de :
- Encontre as raízes de
- Encontre as assíntotas horizontais e verticais de , caso existam
- Identifique os intervalos onde é crescente e decrescente
- Encontre os pontos de máximo e mínimo locais de caso existam
- Identifique os intervalos onde é côncava para cima ou para baixo, e encontre os seus pontos de inflexão, caso existam
- Com base nas informações acima, esboce um gráfico de
Questão 104
4) Considere a função
- Calcule e
- Determine os intervalos de crescimento/decrescimento de , assim como os seus pontos (se existem) de máximo e mínimo absoluto/relativo.
- Determine os intervalos de concavidade para cima/baixo de g, assim como os seus pontos (se existem) de inflexão.
- Usando as informações dos itens anteriores, faça um esboço do gráfico de g, indicando os pontos notáveis obtidos. (Não tente determinar as raízes da função g.)
Questão 107
Q03) Considere a função
Determine caso existam:
- As equações das assíntotas verticais do gráfico de
- As equações das assíntotas horizontais do gráfico de
- As equações das assíntotas oblíquas do gráfico de
- Os intervalos de crescimento e decrescimento de
- Utilizando as informações obtidas nos itens anteriores, esboce o gráfico da função e suas retas assíntotas. Marque em seu desenho as abscissas dos pontos de máximo local e mínimo local do gráfico de , caso existam.
Questão 108
Considere a função
definida para .
- Determine a(s) assíntota(s), calculando os imites necessários.
- Encontre os intervalos de crescimento e decrescimento, bem como extremo(s) local(is).
- Analise a concavidade e encontre os pontos de inflexão.
- Esboce o gráfico
Questão 109
Considere :
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Utilizando as informações obtidas abaixo nos itens anteriores, faça um esboço do gráfico de .
Ver solução completaQuestão 110
Considere a função
(a) Esboce o gráfico da função .
(b) Considere um retângulo satisfazendo as seguintes condições:
- O vértice está no eixo negativo e possui abscissa
- O vértice está no eixo positivo e possui abscissa
- O vértice está no gráfico da função e possui abscissa
- O vértice está no gráfico da função e possui abscissa
(b.1) Escreva as ordenadas dos vértices e em termos de .
(b.2) Determine o domínio e a expressão da função , que fornece o perímetro do retângulo em termos de
Ver solução completaQuestão 111
Considere a função dada por:
(a) Determine caso exista(m):
(a.1) O(s) intervalo(s) de crescimento e decrescimento de
(a.2) O(s) valor(es) de para os quais a função possui máximo local e mínimo local. Atenção: só serão aceitas respostas com justificativas
(b) Determine caso exista(m):
(b.1) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo
(b.2) A(s) abscissa(s) do(s) ponto(s) de inflexão do gráfico de . Atenção: só serão aceitas respostas com justificativas
(c) Faça abaixo um esboço do gráfico de . Indique explicitamente em seu desenho as abscissas dos pontos de máximo, de mínimo e de inflexão determinados nos itens anteriores. Esboce também as retas tangentes ao gráfico de nos pontos em que a derivada é zero e nos pontos de inflexão.
Ver solução completaQuestão 112
Seja uma função derivável tal que:
- ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
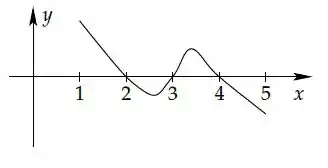
É correto dizer que o número de raízes de no intervalo é
Questão 113
Seja uma função derivável tal que:
- e ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
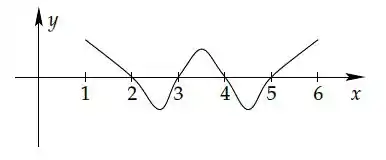
É correto dizer que o número de raízes de no intervalo é
Questão 114
Seja uma função derivável tal que:
- e ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
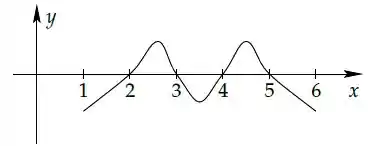
É correto dizer que o número de raízes de no intervalo é
Questão 115
Seja uma função derivável tal que:
- ;
- As retas e são assíntotas para ;
- tem exatamente raízes, e o gráfico de no intervalo está esboçado na figura abaixo
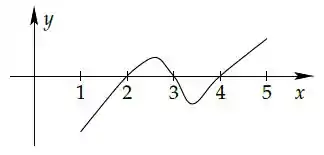
É correto dizer que o número de raízes de no intervalo é
Questão 116
Considere a função .
- Verifique que e que .
- Ache as assíntotas horizontais e verticais caso existam.
- Identifique os intervalos onde a função é crescente e onde é decrescente.
- Encontre os valores de máximo e mínimo locais e/ou globais caso existam.
- Identifique os intervalos de concavidade para cima e para baixo e os pontos de inflexão.
- Usando as informações anteriores faça um esboço do gráfico de
Questão 117
Considere a função .
- Determine as retas assíntotas verticais e horizontais (caso existam), calculando os limites necessários.
- Encontre os intervalos de crescimento e decrescimento, bem como os pontos críticos. Determine os pontos de máximo e mínimos locais, caso existam.
- Analise a concavidade e encontre os pontos de inflexão.
- Esboce o gráfico da função, destacando os pontos críticos e os pontos de inflexão, bem como as retas assíntotas.
Questão 118
Seja uma função tal que . Então podemos afirmar que:
para todo .
.
Existe tal que .
para todo .
.
Ver solução completaQuestão 120
Repita o que foi feito no exercício acima para as funções seguintes.
Ver solução completaQuestão 121
Considere a função
- Determine o domínio, a primeira derivada e estude o crescimento e decrescimento de
- Determine a derivada de segunda ordem, estude a concavidade de e determine os possíveis pontos de inflexão
- Determine, caso exista, os pontos críticos, de máximos locais, máximos globais, mínimos locais, mínimos globais de . Justifique o motivo de ser local ou global.
- Determine as assíntotas e faça o esboço na figura fornecida abaixo
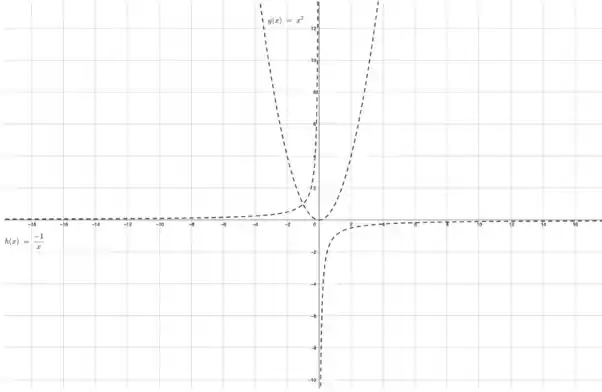
Questão 123
O mecanismo de suspensão dos automóveis consiste num sistema composto de uma mola e de um amortecedor. Denotando por s(t) a posição vertical de um veículo de massa em relação a posição de equilíbrio, temos que a força da mola é dada, pela lei de Hooke, por e a força do amortecedor é dada por , onde é a velocidade instantânea e a constante é denominada viscosidade do amortecedor. Como a força resultante é , pela Segunda Lei de Newton, temos que
para . Suponha que, em unidades adequadas, e e considere
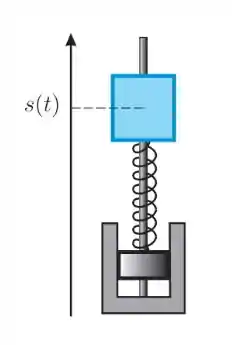
(a) Calcule e e verifique que a equação é satisfeita.
(b) Calcule os pontos críticos de e determine seus extremos
locais e seus intervalos de crescimento e decrescimento.
(c) Determine os pontos de inflexão de e os intervalos
onde a concavidade é voltada para cima e onde é voltada para baixo.
(d) Determine as assíntotas de e, em seguida, esboce o seu gráfico.
Ver solução completaQuestão 124
Dada a função
Determine:
- As raízes reais da função
- Intervalos de crescimento e de decrescimento
- Pontos de máximo relativo (local), pontos de mínimo relativo (local), caso existam
- Intervalos das concavidades para cima e para baixo
- Pontos de inflexão, caso existam
- O esboço do gráfico
Questão 125
Considere a função cujo gráfico é dado na figura abaixo
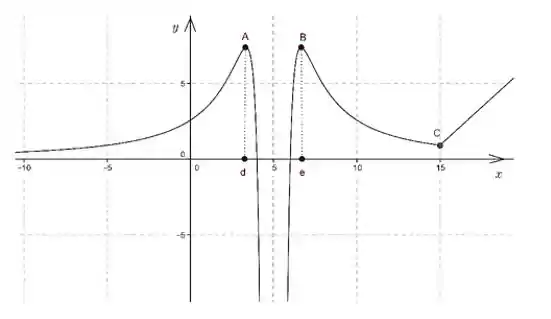
Com a ajuda da figura, responda às seguintes perguntas:
(i) Quais são as assíntotas horizontais e verticais ao gráfico da função ?
(ii) Identifique os intervalos onde a derivada da função é positiva e os intervalos onde a derivada da função é negativa
(iii) Quais são os pontos críticos de ? A função admite máximos ou mínimos locais nesses pontos?
(iv) A função é derivável em ? Caso seja, quanto vale ? A função é derivável em ? Caso seja, quanto vale ?
Ver solução completaQuestão 126
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 127
Seja
Faça um esboço do gráfico de explicitando: domínio, pontos críticos (caso existam), intervalos de crescimento e decrescimento, concavidade, pontos de inflexão (caso existam) e assíntotas verticais e horizontais ou oblíquas (caso existam).
Ver solução completaQuestão 128
Seja a função definida por:
Obtenha, caso existam:
- As assíntotas horizontais e verticais do gráfico de .
- Os intervalos onde é crescente e onde é decrescente.
- Os intervalos onde o gráfico de é côncavo para cima, onde é côncavo para baixo e os pontos de inflexão.
Questão 129
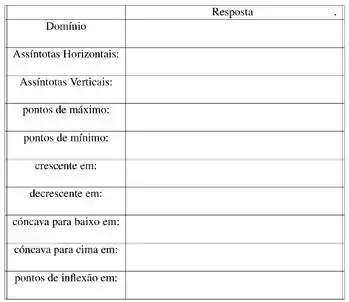
Seja
Complete a seguinte tabela e faça um esboço do gráfico de . Justifique
Questão 130
O gráfico a seguir representa a função contínua e derivável em .
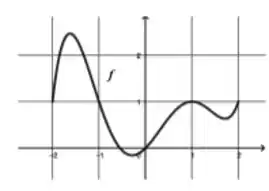
Se no intervalo representado tem pontos críticos e pontos de inflexão, então vale
Questão 131
Considere a funçao definida por:
Sobre as assíntotas do gráfico de f ́é correto afirmar que:
a) são as únicas assíntotas horizontais e é a única assíntotas vertical.
b) é a única assíntota horizontal e é a única assíntotas vertical.
c) é a única assíntota horizontal e não existe assíntotas vertical.
d) são as únicas assíntotas horizontais e não existe assíntota vertical.
e) Não existem assíntotas horizontais e é a única assíntotas vertical.
Ver solução completaQuestão 135
A figura abaixo representa o gráfico de uma função .
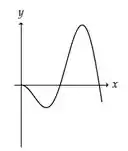
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 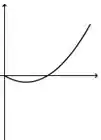
b) 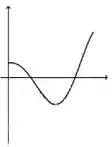
c) 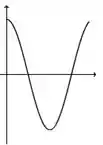
d) 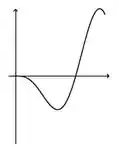
e) 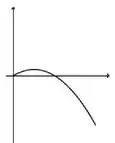
Questão 137
Escreva a equação da reta tangente às curvas no ponto especificado. Esboce o gráfico de e da reta tangente.
Questão 138
4) Considere a função , definida para
a) Determine as retas assíntotas verticais e horizontais (caso existam), calculando os limites necessários
b) Encontre os intervalos de crescimento e decrescimento, bem como os pontos críticos. Determine os pontos de máximo e mínimo locais, caso existam
c) Analise a concavidade e encontre os pontos de inflexão
d) Esboce o gráfico da função, destacando os pontos críticos e de inflexão, bem como as assíntotas
Ver solução completaQuestão 139
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
para todo .
para todo .
Ver solução completaQuestão 140
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 142
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 143
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo, assíntotas verticais. Note que as derivadas já estão dadas.
Ver solução completaQuestão 144
Seja ; . Prove (usando derivação) que ou prove (usando teoremas de continuidade) que existe um número , tal que
Ver solução completaQuestão 145
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 146
Um determinado sistema tem sua capacidade variando com um parâmetro através de dois modelos definidos dependentes do valor de . Quando é não-negativo sabe-se que , e quando é negativo sabe-se que . Você é o engenheiro responsável e precisa entender o total funcionamento do sistema com a variação do parâmetro . Com isso:
- Faça o esboço do modelo completo da capacidade do sistema para a variação de em todo . (Obs.: Devem ser apresentados todos os cálculos antes do desenho do esboço, englobando todos os passos vistos em teoria em sala).
- Os pontos críticos obtidos na capacidade do sistema quando varia em todo .
- Os pontos de inflexão obtidos na capacidade do sistema quando varia em todo .
- Sabendo que o sistema funcionará apenas para e , determine, caso existam, os máximos e mínimos globais para cada um dos intervalos de funcionamento.
Questão 147
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 148
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 149
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 150
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 151
Repita o que foi feito no exercício acima para as funções seguintes.
Ver solução completaQuestão 152
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 153
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo. Determine as (possíveis) assíntotas e, finalmente, faça um esboço do gráfico da função.
Ver solução completaQuestão 155
3) repita o que foi feita no feito no exercício acima para as funções seguintes;
d)
Ver solução completaQuestão 156
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
c)
para e para ,
para e para .
para ,
para e para .
Ver solução completaQuestão 157
Seja
Com e . Determine, caso existam:
definida para .
- Assíntotas horizontais e verticais do gráfico de
- intervalos onde é crescente e intervalos onde é decrescente
- pontos críticos de
- máximos locais e mínimos locais
- intervalos onde o gráfico de é côncavo para cima e intervalos onde o gráfico de é côncavo para baixo
- pontos de inflexão do gráfico de
- utilizando os resultados dos itens anteriores, esboce o gráfico de
Questão 159
Para cada uma das funções abaixo, determine: pontos críticos, máximos e mínimos locais, intervalos de crescimento e decrescimento, pontos de inflexão, intervalos onde f é côncava para cima e para baixo, assíntotas verticais. Note que as derivadas já estão dadas.
Ver solução completaQuestão 160
3) repita o que foi feita no feito no exercício acima para as funções seguintes;
e)
Ver solução completaQuestão 165
O gráfico da derivada é dado a seguir:
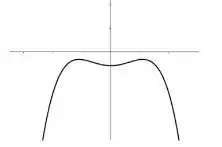
Qual das seguintes alternativas corresponde ao gráfico de ?
Ver solução completaQuestão 166
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 167
A figura mostra os gráficos de . Identifique cada curva e explique suas escolhas.
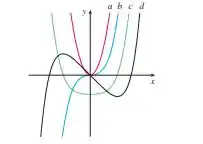
Questão 168
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 169
Seja dada por
- Determine s equações das retas assíntotas horizontais do gráfico de , caso existam.
- Determine s equações das retas assíntotas verticais do gráfico de , caso existam.
- Determine os intervalos de crescimento e de decrescimento de .
- Esboce o gráfico de e suas retas assíntotas horizontais e verticais, caso existam. Marque em seu esboço as abscissas dos pontos de máximo e mínimo local de , caso existam.
- Determine todos os valores para os quais a equação possui ao menos uma solução real
Questão 172
Considere a função
cujas derivada e derivada segunda são dadas por:
- Calcule o domínio de definição de .
- Calcule as interseções do gráfico de com os eixos coordenados caso existam.
- Calcule os limites de no infinito e ache as assíntotas horizontais e verticais ao gráfico de caso exista.
- Identifique os pontos críticos, os extremos relativos e os intervalos onde a função é crescente e onde é decrescente.
- Identifique os pontos de inflexão da função e os intervalos de concavidade para cima e para baixo.
- Usando as informações anteriores, faça um esboço do gráfico de .
Questão 174
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 175
3. Uma função satisfaz as seguintes propriedades:
- e
- é estritamente crescente em e
- é uma função par
- Esboce o gráfico de uma tal função.
Questão 176
3) Use o roteiro feito em aula para esboçar a curva . Indique todos os passos do roteiro, isto será tomado em conta na avaliação.
Ver solução completaQuestão 177
3) Esboce o gráfico de uma função que satisfaça as seguintes condições:
- é contínua em todo o seu domínio
- é crescente nos intervalos e
- é decrescente no intervalo
- é crescente nos intervalos e
- é decrescente no intervalo
Passo 1
Essa questão facilita a nossa vida no esboço porque ela nos dá tudo, viu? Só vamos precisar interpretar direitinho. Então bora lá. Vamos começar com o domínio:
Veja então que a função está definida para qualquer real menos . Graficamente, isso quer dizer duas coisas:
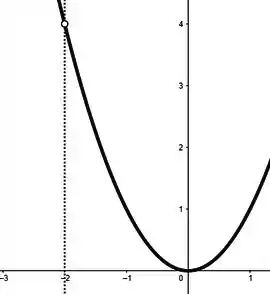
Ou a função tem essa cara e simplesmente não está definido...
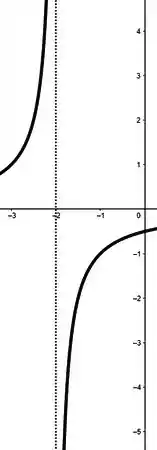
...ou é uma assíntota vertical! Já deu pra ver que vamos precisar ficar de olho nas assíntotas né? Então vamos buscar elas
Passo 2
Beleza. Pra buscar assíntotas, temos que lembrar que precisamos fazer limites. Então vou trazer de volta alguns dos limites do enunciado.
Mas porque estamos olhando só pra esses dois? Porque, veja bem, em uma função sem assíntotas nenhuma, nem vertical nem horizontal, seja pertencente ao domínio de :
Agora, se existem assíntotas verticais, o limite para tendendo ao número, vai ser infinito ou menos infinito e se existem assíntotas horizontais, o limite pros infinitos serão números. Show, se:
Então de fato:
E veja bem, se se aproxima de pela esquerda (valores menores que ), o limite é diferente do se aproximando pela direita (valores maiores). Sendo a função ainda, segundo o enunciado, crescente nos intervalos e , acaba que, graficamente, temos algo semelhante à:
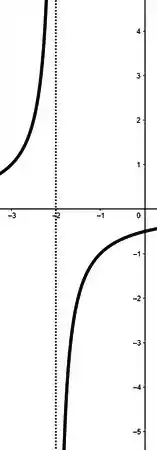
Show, agora vamos ver as assíntotas horizontais. Temos sim informações sobre elas ó:
Maravilha, nossa única assíntota horizontal vai ser então:
E usando essas informações, já da pra fazer um pré esboço:
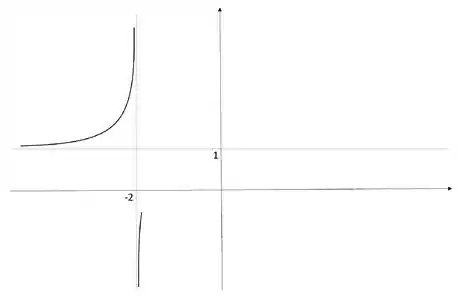
Passo 3
Ok, mas não sentiu falta de um limite não? O que faremos com esse aqui:
A primeira coisa que podemos notar nesse limite, é que se pertence ao domínio de , então:
Opa, não é que o limite que faltou se encaixa nesse modelo? Podemos afirmar então que:
É um ponto da nossa curva. Vamos marcar ele então no nosso esboço:
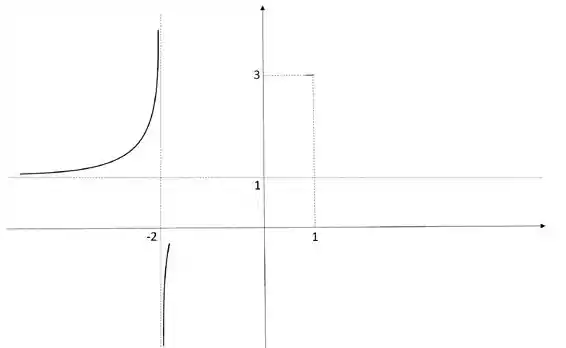
Passo 4
Pra fechar, vamos olhar pras informações sobre intervalo de crescimento e decrescimento
Ou seja, saindo de a função tem que crescer até alcançar o ponto que a gente já sabe que ele passa:
O esboço vai ficar:
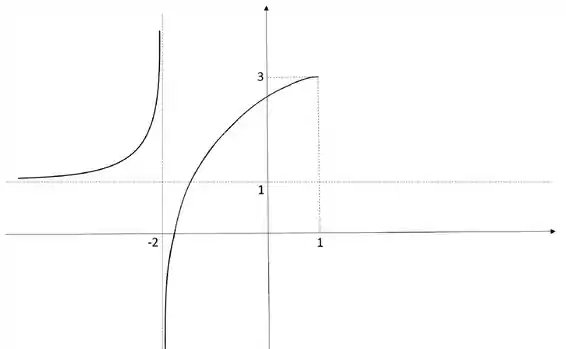
E depois desse ponto, como a função decresce, traçamos uma linha até , assíntota horizontal, mas sem nunca tocar nela, ok?
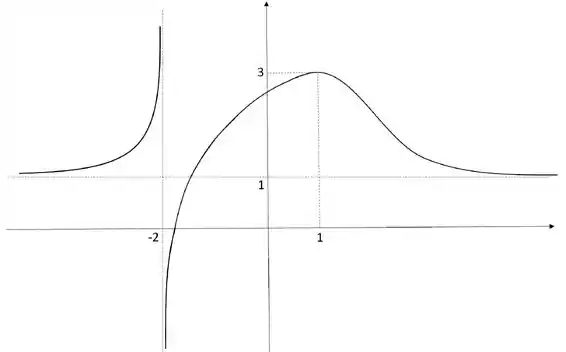
E taí! Questão finalizadíssima. Agora é só partir pro abraço.
Ver solução completaQuestão 178
- Considere a dada por e suas derivadas e
f. Faça o esboço do gráfico de , identificando, caso existam, as assíntotas, os pontos de máximo e mínimo e os pontos de inflexão.
Ver solução completaQuestão 180
Considere
- Verifique que
- Ache as assíntotas horizontais e verticais caso existam.
- Identifique os intervalos onde a função é crescente e onde é decrescente.
- Encontre os valores máximo e mínimo locais e/ou globais caso existam.
- Identifique os intervalos de concavidade para cima e para baixo e os pontos de inflexão
- Usando as informações anteriores faça um esboço do gráfico de
e que
Questão 181
Encontre as assíntotas verticais e horizontais da seguinte função
Depois faça um esboço do gráfico de .
Ver solução completaQuestão 182
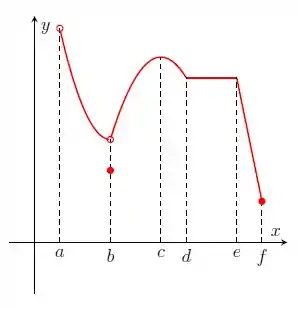
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
Questão 183
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 184
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 185
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 186
Considere a função .
Determine:
os limites de quando tende a e quando tende a ;
os intervalos onde é crescente e aqueles onde é decrescente;
os pontos de máximo e mínimo locais e/ou globais (abscissas e ordenadas);
os intervalos onde a concavidade é para cima (função é convexa) e aqueles onde é para baixo (função é côncava);
os pontos de inflexão de .
Esboce o gráfico de , respeitando todos os aspectos do gráfico identificados no item .
Ver solução completaQuestão 187
Encontre, se existirem, as assíntotas horizontais e verticais do gráfico da função e esboce o seu gráfico.
Ver solução completaQuestão 188
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 189
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 190
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 191
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 192
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 195
Use o roteiro a seguir para esboçar o gráfico
- Dê o domínio de
- Estude os intervalos onde é crescente ou decrescente, destacando os pontos críticos
- Encontre os máximos ou mínimos locais ou absolutos, se existirem
- Estude a concavidade, destacando os pontos de inflexão
- Encontre as assíntotas horizontais ou verticais, se existirem
- Esboce o gráfico
Questão 196
Na teoria da relatividade, a massa de uma partícula é
Em que é a massa de repouso da partícula, é a massa quando a partícula se move com velocidade em relação ao observador e é a velocidade da luz. Esboce o gráfico de como uma função .
Ver solução completaQuestão 197
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 198
4) Considere a função , sendo suas derivadas primeira e segunda dadas, respectivamente, por e . Siga o roteiro abaixo para esboçar um gráfico de :
- Encontre as raízes de
- Encontre as assíntotas horizontais e verticais de , caso existam
- Identifique os intervalos onde é crescente e decrescente
- Encontre os pontos de máximo e mínimo locais de caso existam
- Identifique os intervalos onde é côncava para cima ou para baixo, e encontre os seus pontos de inflexão, caso existam
- Com base nas informações acima, esboce um gráfico de
Questão 199
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 200
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaQuestão 201
4. Considere a função cujo gráfico está representado abaixo.
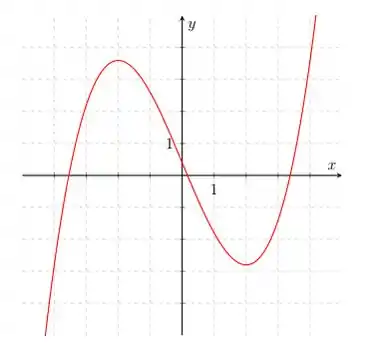
Estabeleça a ordem de crescimento dos números e .
Ver solução completaQuestão 202
Considere :
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Esboce o gráfico da função.
Ver solução completaQuestão 205
Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Questão 207
6. Uma folha de papelão mede . Dois quadrados iguais, de lado , são recortados dos vértices de um lado com , como mostra a figura. Dois retângulos iguais são recortados dos outros vértices, de modo que as abas possam ser dobradas para formar uma caixa retangular com tampa.
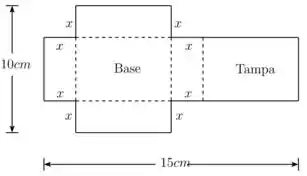
(a) Escreva uma fórmula para o volume da caixa.
(b) Determine o domínio de .
(c) Determine o valor de para que o volume da caixa seja o maior possível.
Ver solução completaQuestão 208
Seja
(e) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c), justificando.
Ver solução completaQuestão 209
Seja
(e) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c), justificando.
Ver solução completaQuestão 210
Seja
(d) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c), justificando.
Ver solução completaQuestão 211
Dada a função , explicite o domínio, intervalos de crescimento e decrescimento, concavidade e pontos de inflexão. Finalmente, esboce o gráfico, indicando os pontos importantes que você encontrou.
Ver solução completaQuestão 212
Seja a função definida por .
(a) Encontre as assíntotas verticais e horizontais caso existam;
(b) Encontre os intervalos onde a função é crescente e onde é decrescente;
(c) Encontre os valores de máximo e mínimo locais;
(d) Encontre os intervalos de concavidade e os pontos de inflexão
(e) Use as informações acima para fazer um esboço do gráfico de
Ver solução completaQuestão 216
4) Dada a função , explicite o domínio, intervalos de crescimento e decrescimento, concavidade e pontos de inflexão. Finalmente, esboce o gráfico, indicando todos os pontos importantes que você encontrou.
Ver solução completaQuestão 217
Considere
é contínua em ? é derivável em ?
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Ver solução completaQuestão 218
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
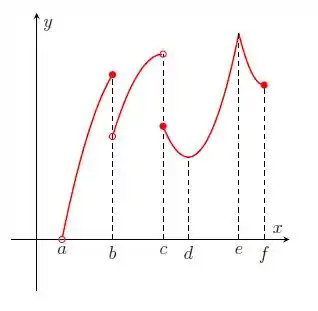
Questão 219
Considere a função . Determine:
O domínio de ;
Os interceptos;
As simetrias de ;
As assíntotas;
Intervalos de crescimento e decrescimento;
Valores máximos e mínimos locais;
Discuta concavidade e dê os pontos de inflexão;
Use a informação obtida para esboçar o gráfico de .
Ver solução completaQuestão 220
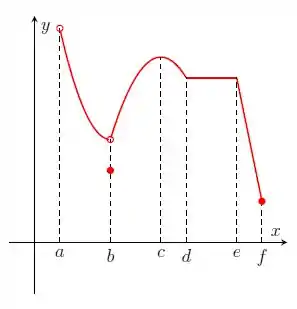
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
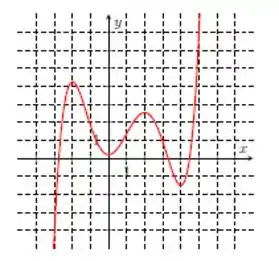
Questão 221
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
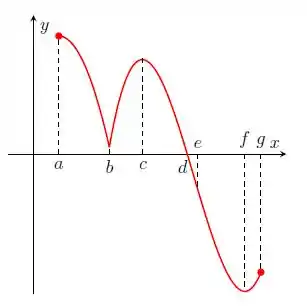
Questão 222
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
Questão 223
A função , aparece em aplicações para a sintetização de frequência modulada (FM).
(b) Calcule f′(x) e utilizando uma calculadora gráfica plote seu gráfico. Compare com o obtido no item (a).
Ver solução completaQuestão 224
Suponha que o número de milhares de pessoas infectadas por um vírus seja modelado pela função em que e são constantes e o tempo é medido em anos. Suponha ainda que, no instante , nove mil pessoas estavam infectadas, uns anos depois esse número atingiu um valor mínimo e, em seguida, cresceu até atingir um valor máximo para .
Determine as constantes e a partir das informações dadas.
Determine o número de pessoas infectadas anos depois do instante .
Determine a concavidade de e, em seguida, esboce o seu gráfico para
Ver solução completaQuestão 225
Conforme ilustra a figura abaixo, as áreas dos retângulos inscritos na circunferência podemos ser calculadas por meio da função , com
- Calcule os pontos críticos da função no intervalo
- Determine os intervalos de crescimento e os de decrescimento da função
- Determine os intervalos em que a concavidade do gráfico de é voltada para baixo e os intervalo em que a concavidade é voltada para cima
- Esboce o gráfico de
Questão 226
Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:
(a)
Ver solução completaQuestão 227
Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:
(b) f ′ (x) > 0 para x 0;
Ver solução completaQuestão 228
Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:
(c) f” (x) > 0 para x 0 para x > 0;
Ver solução completaQuestão 229
Durante o processo de tosse, provocado pela presença a traqueia de algum corpo estranho, a traqueia se contrai com o objetivo de aumentar o fluxo de ar através dela, e assim tornar mais eficiente o método de expulsão do corpo estranho. Segundo Pouseiulle, indicando por o raio da traqueia em estado normal e por o seu raio durante a tosse, o fluxo de ar na traqueia pode ser modelado por:
Onde K é uma constante positiva.
- Determine os pontos críticos de no intervalo
- Determine os intervalos de crescimento e de decrescimento de
- Determine os intervalos em que o gráfico de é côncavo para cima ou para baixo.
- Use os itens anteriores para esboçar o gráfico de no caso em que
Questão 230
Considere duas cargas elétricas com carga unitária e positiva, fixadas num eixo perpendicular a uma parede, como na figura abaixo. O potencial elétrico gerado por essas duas partículas num ponto ao longo desse eixo é dado, em unidades convenientes, pela
seguinte função
(a) Verifique que o potencial elétrico é dado por
(b) Calcule a força exercida numa partícula de carga unitária posicionada em , dada
por .
(c) Calcule os pontos críticos de e determine seus extremos locais e seus intervalos
de crescimento e decrescimento. A força se anula em algum ponto?
(d) Determine os pontos de inflexão de e seus intervalos de concavidade para cima
e para baixo.
(e) Determine as assíntotas verticais e horizontais de e esboce seu gráfico.
Ver solução completaQuestão 231
Seja
- Determine o domínio da função
- Calcule a derivada da função
- Determine todas as assíntotas da curva . Calcule todos os limites necessários e justifique suas respostas.
- Esboce o gráfico de
Questão 232
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 233
Considere a função: .
Indique seu domínio e os interceptos.
Encontre os seus extremos, classifique-os e indique onde a função é crescente ou decrescente.
Indique onde a função tem concavidade para cima ou para baixo e determine seus pontos de inflexão, caso existam.
Esboce o gráfico da função.
Ver solução completaQuestão 234
Uma função tem as seguintes propriedades
-
i) é crescente em _____ e decrescente em ______ .
ii) ́ é côncava para cima em _____ e côncava para baixo em _____ .
iii)́ ______ é um ponto de máximo local e ___________ é um ponto de inflexão do gráfico de .
- Esboce o gráfico de
Questão 235
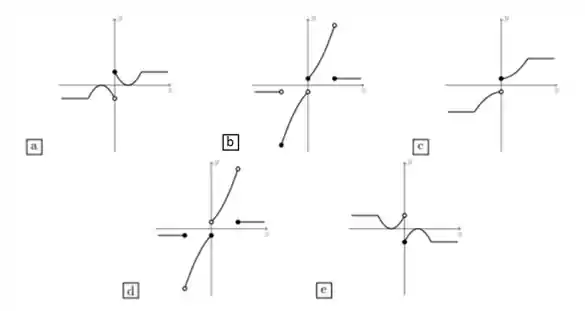
9. Considere as funções , definidas por
E
A figura que melhor representa o gráfico de é:
Questão 236
Considere
é contínua em ? é derivável em ?
Calcule e .
Determine os pontos críticos de .
Em quais intervalos é crescente?
Em quais intervalos é decrescente?
Determine, se houver, os pontos de mínimo local de .
Determine, se houver, os pontos de máximo local de .
Em quais intervalos, se houver, o gráfico de é côncavo para cima?
Em quais intervalos, se houver, o gráfico de é côncavo para baixo?
Determine, se houver, os pontos de inflexão do gráfico de .
Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .
Ver solução completaQuestão 237
Seja uma função tal que . Então podemos afirmar que:
para todo .
.
Existe tal que .
para todo .
.
Ver solução completaQuestão 238
Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-
cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso
existam).
Ver solução completaQuestão 239
Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-
cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso
existam).
Ver solução completaQuestão 240
Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-
cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso
existam).
Ver solução completaQuestão 241
Considere a função
a) Esboce o gráfico de , determinando:
- Os intervalos onde é crescente ou decrescente;
- Os seus máximos e mínimos locais;
- Os intervalos onde a concavidade é para cima ou para baixo.
b) Determine o número de raízes distintas de (isto é, para quantos valores distintos de tem-se . Justifique sua resposta.
Ver solução completaQuestão 242
Seja .
- Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo e mínimo
- Determine os intervalos onde é côncava pra cima/baixo e os seus pontos de inflexão
- Caso existam, encontre as assíntotas horizontais e verticais de
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens e
Questão 243
Considere a função dada por:
Determine caso exista(m):
(a.1) O(s) intervalo(s) de crescimento e decrescimento de
(a.2) O(s) valor(es) de para os quais a função possui máximo local e mínimo local.
(b.1) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
(b.2) O(s) ponto(s) de inflexão do gráfico de .
(c) Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão determinado(s) nos itens anteriores. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão
(d) A equação sempre possui solução? Justifique sua resposta.
Ver solução completaQuestão 244
Considere a função , cujo domínio é o maior intervalo poss��vel para que seja inversível e para que o gráfico de (a função inversa de ) passe pelo ponto
- Determine o domíno de e de
- Determine uma expressão para
- Esboce abaixo a reta e os gráficos das funções e (em seus respectivos domínios)
Questão 245
A figura abaixo representa o gráfico de uma função .
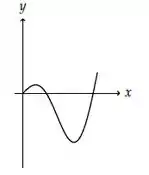
A figura que mais se aproxima do gráfico de uma primitiva de é:
a) 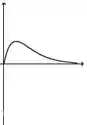
b) 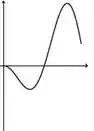
c) 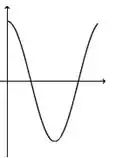
d) 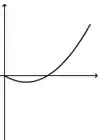
e)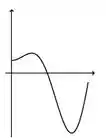
Questão 246
Considere uma função \ com as seguintes propriedades:
- , para todo no domínio da função;
- ;
- para e para ;
- e ;
- e .
Faça um esboço do gráfico dessa função.
Ver solução completaQuestão 248
Seja
Pede-se:
.
Intervalos de crescimento e decrescimento, máximos e mínimos locais.
Concavidade e pontos de inflexão.
Assíntotas.
Esboço do gráfico.
Imagem de .
Ver solução completaQuestão 249
Seja
a) Determine os intervalos de crescimento e decrescimento de
b) Determine os pontos de máximo e de mínimo de
c) Determine todos os pontos de inflexão de
Ver solução completaQuestão 252
Considere a seguinte função
Encontre o domínio de , os pontos de interseção do gráfico de com os eixos e analise a simetria de .
Caso existam, determine as assíntotas horizontais e verticais de .
Determine os intervalos de crescimento e decrescimento de , seus pontos de máximo e mínimo e os seus valores.
Determine os intervalos onde tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de usando as informações obtidas nos itens anteriores.
Ver solução completaQuestão 253
2) Seja uma função duas vezes diferenciável em seu domínio tal que:
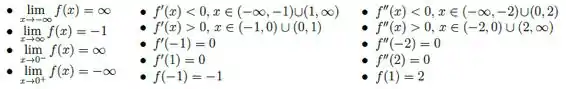
- Faça um esboço do gráfico de , indicando claramente as regiões de crescimento e decrescimento, os pontos extremos relativos, os pontos extremos absolutos, assíntotas, concavidade do gráfico e pontos de inflexão.
- A função tem quantas raízes em ? E em ? (Se não houver informação suficiente para se determinar a quantidade exata de raízes, indique quais são as quantidades possíveis). Justifique.
Questão 255
Seja duas vezes diferenciável e tal que
• , e
•, , ,
• se e se
• o gráfico de está dado abaixo
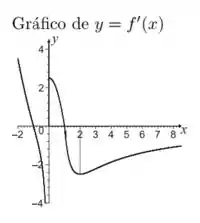
Nestas condições,
(a) prove que
(b) prove que
(c) esboce um possível gráfico de
Ver solução completaQuestão 256
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 257
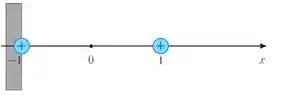
Aplicando os conceitos da primeira e segunda derivadas. Qual o gráfico da função definida em por ?
(a)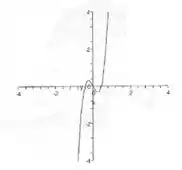
Questão 258
Escreva a equação da reta tangente às curvas no ponto especificado. Esboce o gráfico de e da reta tangente.
Questão 259
Escreva a equação da reta tangente às curvas no ponto especificado. Esboce o gráfico de e da reta tangente.
Questão 260
Escreva a equação da reta tangente às curvas no ponto especificado. Esboce o gráfico de e da reta tangente.
Questão 261
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 268
Seja :
Mostre que e que .
Encontre o domínio de .
Encontre os interceptos de com os eixos coordenados.
Analise a simetria de .
Caso existam, encontre as assíntotas horizontais e verticais de .
Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo/mínimo.
Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
Esboce o gráfico de usando as informações obtidas nos itens anteriores.
Ver solução completaQuestão 269
Considere as funções deriváveis e cujos gráficos estão esboçados abaixo:
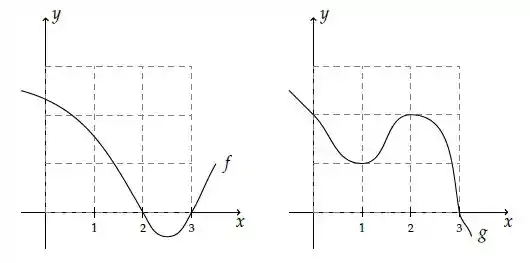
Seja . Sabendo que é ponto de mínimo local de e que , é correto afirmar que
- é ponto de inflexão de
- é ponto de mínimo local de
- é ponto de máximo local de
Questão 270
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades
Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.
Ver solução completaQuestão 271
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades
Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.
Ver solução completaQuestão 272
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 273
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 274
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 275
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 276
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 277
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 278
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 279
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 280
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 281
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 282
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 283
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 284
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 285
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 286
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 287
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 288
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 289
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 290
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 291
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 292
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 293
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 294
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 295
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 296
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 299
O gráfico da função derivada f′ de uma função contínua f é dado abaixo.
e) Supondo que f (0) = 0, esboce o gráfico de f
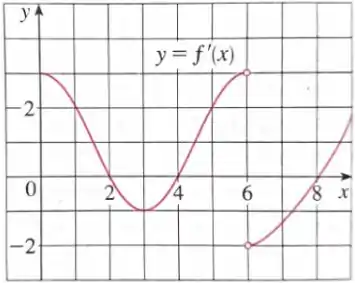
Questão 301
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Ver solução completaQuestão 302
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
b) é uma assíntota vertical, para para , para .
Ver solução completaQuestão 303
Seguindo o roteiro anterior, esboce os gráficos das funções dadas a seguir.
Ver solução completaQuestão 304
Seguindo o roteiro anterior, esboce os gráficos das funções dadas a seguir.
Ver solução completaQuestão 306
Seguindo o roteiro anterior, esboce os gráficos das funções dadas a seguir.
Ver solução completaQuestão 307
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
(d) para todo ,
é uma assíntota vertical,
para e para ,
para
Ver solução completaQuestão 308
A função , aparece em aplicações para a sintetização de frequência modulada (FM).
(a) Use uma calculadora gráfica para esboçar um gráfico da função f (x), em seguida, use esse gráfico para dar um esboço, mesmo que grosseiro, do gráfico de sua derivada f ′ (x).
Ver solução completaQuestão 312
2) Esboce o gráfico de
Considerando: domínio, interseções com os eixos, limites necessários, regiões de crescimento e decrescimento, máximos e mínimos, regiões de concavidade e pontos de inflexão.
Ver solução completaQuestão 314
Esboce o gráfico da função e dê explicitamente o que se pede:
- Domínio de
- Paridade de
- Equações das assíntotas verticais e horizontais do gráfico
- Intervalos de em que é contínua
- Pontos de em que a tangente ao gráfico é vertical
- Intervalos de onde é crescente e onde é decrescente
- Extremos relativos de e os respectivos pontos de onde ocorrem
- Intervalos onde a concavidade do gráfico é para cima, onde é para baixo e seus pontos de inflexão;
- Extremos absolutos de e os respectivos pontos de onde ocorrem;
- Imagem de
Questão 315
Faça o gráfico de cada uma das funções abaixo e, a partir do gráfico, determine (quando houver) pontos de máximo/mínimo locais/absolutos e máximos/mínimos locais/absolutos.
Ver solução completaQuestão 316
Seja
a) Determine o domínio da função
b) Determine as equações das retar assíntotas verticais do gráfico de , caso existam.
c) Mostre que a reta é assíntota oblíqua do gráfico de para a direita (ou seja, quando )
d) Sabendo que é crescente em todo o seu domínio e que a reta é assíntota obliqua do gráfico de para os dois lados (ou seja, quando e ), esboce abaixo o gráfico de e suas retar assíntotas verticais, caso existam.
Ver solução completaQuestão 319
Seja
Determine o domínio de
Determine os intervalos de crescimento e os intervalos de decrescimento de
Determine os pontos de máximo e de mínimo de
Determine todas as assíntotas da curva
Determine todos os pontos de inflexão de
Esboce o gráfico de contemplando tudo que foi calculado acima
Considere agora a função A respeito do domínio de , o que se pode afirmar? Escolha uma das opções abaixo e justifique adequadamente a sua resposta.
O domínio é
O domínio é
O domínio é
O domínio é onde
Ver solução completa