Considere a equação . Verifique que a mudança de variável , a transforma em e resolva. (Observe que a equação dada já é uma equação de Bernoulli, a mudança de variável apenas simplifica a resolução.)
Passo 1
Vamos lá galera! Essa já é conhecida! Para solução , as soluções não constantes são dadas implicitamente por:
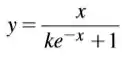
Isso acontece por causa das relações de Bernoulli dentro das EDO’s que a gente faz muitas vezes, então ela acaba virando uma daquelas equações que de cara, a gente já vê, manja e lembra da resposta, que pode até ser tratada como uma identidade para assuntos como Integral de Cauchy e Riemann lá nos números complexos!