Descreva um processo para se avaliar com erro inferior, em módulo, a
Passo 1
Boom, vamos continuando a questão 10!!
Para avaliar podemos usar a relação da letra a:
Se
Então nós precisamos achar a ok?
Se lembrarem que:
Então:
Para calcular o somatório eu vou usar o Excel, ok?
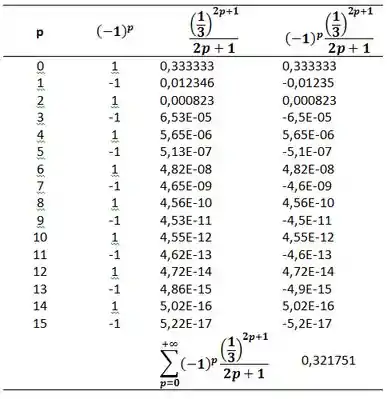
Então:
Agora é só substituir:
Comparando o valor obtido aqui do valor da calculadora:
1,249046
Vocês podem estar se perguntando porque já não fiz o somatório direto, não é?
Mas o somatório só é válido para
Agora que entendemos isso podemos seguir !!