Enunciado
Cálculo - James Stewart - Vol 2- Ed: 6º - Capítulo 16.6 - Ex. 43
Determine a área da superfície.
A parte do parabolóide hiperbólico que está entre os cilindros e
Passo 1
Olá, tudo bem?
Bom, esse exercício quer que a gente ache a area da superficie da parte do parabolóide hiperbólico que está entre os cilindros e .
Para determinar a área de uma superfície devemos fazer:
Onde a função é uma função das variáveis e , dentro da região no plano .
Aqui a função é:
Beleza, agora o que precisamos fazer para resolver essa questão é mudar a função para coordenadas polares , já que se trata de uma região entre círculos.Depois disso iremos achar os novos limites de integração, beleza?
Calma que está quase no final, o próximo passo será achar as derivadas parciais e e depois só substituir e resolver a integral.
Vamos lá!
Passo 2
Sabemos que as coordenadas polares são escritas da seguinte forma:
Iremos substituir os valores depois de acharmos a derivada parcial!!
Vamos achar os limites de integração. O enunciado nos diz que parte do parabolóide estará entre os cilindros :
e
Então os limites são:
Já que a equação do cilindro será:
E para :
Já que a gente quer que percorra toda a região do cilindro, teremos que dar uma volta completa na circunferência, vamos relembrar os ângulos:
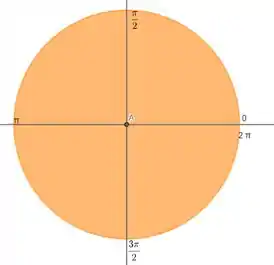
Então o diferencial de área vai ser e o intervalo:
Passo 3
Agora temos que calcular os valores de e .
Já sabemos que a nossa função é:
Suas derivadas parciais são:
e
Perfeito, lembra que eu disse que iríamos substituir os valores parametrizados depois de acharmos as derivadas parciais?? Então vamos lá.
Como:
Logo:
e
Passo 4
Agora que temos que:
Vamos substituir em:
Assim temos:
Se colocarmos o em evidência e lembrando que
Logo:
Passo 5
Já temos uma parte da nossa integral montada sendo:
Agora vamos incluir os limites de integração e :
Logo:
Vamos resolver?
Passo 6
Primeiro vamos escrever essa raiz de outra forma:
Beleza, sempre começamos pelo primeiro diferencial , tá?
Para resolver vamos precisar utilizar o método de substituição:
Substituindo na nossa integral:
Vamos cortar o e colocar a constante para fora:
Agora ficou mais fácil.
Vamos substituir
Vamos por esse em evidência e resolver as contas:
Logo:
Passo 7
Bom, agora a nossa integral passou disso:
Para isso, depois de substituirmos o valor:
Antes de começarmos podemos passar tudo que é constante para fora:
Essa é mais fácil de resolver:
Assim:
Vamos pra próxima?