Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Entender como esse gráfico se comporta é o primeiro passo de tudo! . Bom, a função tem o formato beeem parecido com o da função , que é uma parábola, né?
Já a função são duas retas:
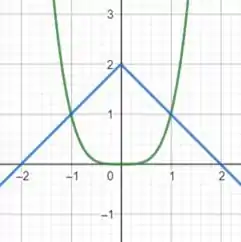
Passo 2
Agora, fazendo a interseção entre as funções, temos dois casos:
Primeiro caso é quando :
Me perdoooa, mas vamos precisar fazer umas mágicas que os matemáticos fazem. Vamos fazer aparecer um (pra tentar usar a diferença de quadrados, lembra? ). Então a gente fez aparecer o negativo, então tem que ter também o positivo pra não alterar a equação.
Agora repara na segunda parte ()... Essa é uma equação de segundo grau, então conseguimos achar as raízes: (calmaa que queremos só achar as raízes pra poder escrever da forma )
Usando Bhaskara mesmo:
Então podemos reescrever:
Voltando lá pra equação:
Colocando o em evidência:
Então temos ou:
(Que é o nosso ponto de interseção mesmo. Temos spoiler no gráfico).
Ou:
Maaaass repara que o pra essa equação dar zero o teria que ser negativo e não interessa a gente, pois estamos no caso em que .
Passo 3
Para o segundo caso que é quando :
Vamos fazer a mesma ladainha. Fazendo aparecer :
Então:
E não queremos porque o deveria ser maior que zero, maas estamos no caso em que .
Então temos que os pontos de interseção são:
E esse vai ser nosso intervalo de integração:
Passo 4
Organizando a integral, temos:
Tem um bendito módulo dentro da integral... E agora, José???
Não piraa... A gente só vai precisar dividir em dois casos também. (dividir em duas integrais e atenção nos intervalos de integração, ok?
Resolvendo...
Então, isso resultará em:
Prontinho!!