Nos Exercícios de 13 a 32, faça um esboço do gráfico da função dada, determinando primeiro o seguinte: os extremos relativos de ; os pontos de inflexão do gráfico de ; os intervalos nos quais é crescente e aqueles onde é decrescente; onde o gráfico é côncavo para cima e onde é côncavo para baixo; a inclinação das tangentes inflexionais, as assíntotas horizontal, vertical e oblíqua, se existirem.
Passo 1
É fácil e importante perceber que são pontos que não pertencem ao domínio da função, pois esses valores de anulam o denominador.
Impossível!
Passo 2
Vamos determinar as raízes reais da função :
A função possui apenas uma raiz real.
Passo 3
Calcular :
Calculando as raízes reais de :
Passo 4
Calculando teremos:
Calculando as raízes reais de :
Essa equação não possui raiz real, ou seja, não existe nenhum ponto no domínio de tal que a segunda derivada seja nula.
Passo 5
Vamos agora analisar cada um dos intervalos notáveis para estudar o sinal das funções , e para determinar pontos de extremo relativo, inflexão, onde a função é crescente e onde o gráfico é côncavo para cima.
Passo 6
Determinando as assíntotas da função:
- Horizontal:
Logo, a função tem uma assíntota horizontal em .
- Vertical:
Logo, a função possui duas assíntotas verticais, uma em e outra em .
- Oblíqua:
Como , percebe-se que a função não possui assíntotas oblíquas.
Passo 7
Observação: como a função não possui pontos de inflexão, não é possível calcular a inclinação da tangente inflexional.
Passo 8
Perceba que, como zero é um máximo relativo e existem assíntotas horizontais em quando tende a , a imagem da função é:
Resposta
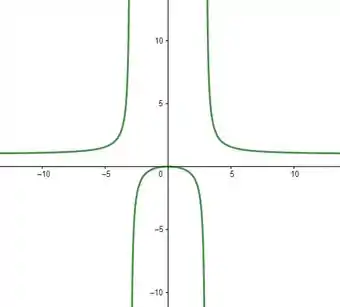
Gráfico: