Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.3 - Ex. 5

Nos Exercícios 5-10, determine as trajetórias ortogonais da família de curvas. Esboce vários membros de cada família.

y = m x

Passo 1

Primeiro iremos calcular o coeficiente angular da reta tangente em questão. Assim teremos que:

y = m x ⇒ m = y x

d d x m = d d x y x

d d x m = d d x y ⋅ x - 1

0 = d d x y x - 1 + y d d x x - 1

d y d x x - 1 - y x - 2 = 0

d y d x 1 x - y x 2 = 0

d y d x 1 x = y x 2 ⇒ d y d x = y x

Passo 2

O coeficiente angular ortogonal a trajetória da reta tangente deve ser negativa e recíproca. Logo o novo coeficiente angular será dado por:

d y d x = - x y

Passo 3

Essa equação ordinária é uma EDO separável. Podemos resolvê-la integrando em ambos os lados. Assim:

d y d x = - x y

y d y = - x d x

∫ y d y = - ∫ x d x

x 2 2 + y 2 2 = c ⇒ E q u a ç ã o   d a   C i r c u n f e r ê n c i a   d e   r a i o   2 c

Passo 4

As famílias de curvas terão o seguinte esboço:

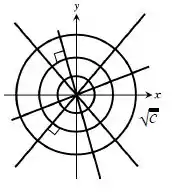
No qual as trajetórias são ortogonais a circunferência.

Resposta

As trajetórias serão ortogonais a curva da circunferência, interceptando-a perpendicularmente. A equação da circunferência é dada por:

x 2 2 + y 2 2 = c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas 1-26, encontre as trajetórias ortogonais da família de curvas dada. y = x 1 + c 1 . x
Nos Problemas 1-26, encontre as trajetórias ortogonais da família de curvas dada. x 2 + y 2 = 2 c 1 x
Nos Problemas 1-26, encontre as trajetórias ortogonais da família de curvas dada. y 2 - x 2 = c 1 x ³ ³
Nos Problemas 1-26, encontre as trajetórias ortogonais da família de curvas dada. y = 1 c 1 + x
Nos Problemas 1-26, encontre as trajetórias ortogonais da família de curvas dada. x 1 3 + y 1 3 = c 1