Nos exercícios 7 a 17, faça um esboço do cilindro de equação dada
17.
Passo 1
Oiii a todos que estão ingressando no mundo do cálculo de várias variáveis. Quando aprendemos a fazer gráficos em cálculo 1, aprendemos vários truques. Inclusive, se você já está mais sagaz, de olhar para uma função e concluir “ah isso aqui, tem um jeito de círculo”, por exemplo, rs. Se você ainda não pegou essa sagacidade, relaxe! Isso vem apenas com o tempo e após vários exercícios.
Quando temos uma equação e vemos em 3D temos que prestar atenção em quantas variáveis estamos lidando! Se só temos 2 isso significa que nossa superfície será uma espécie de cilindro. Teremos aquela curva bonita no plano das duas variáveis, e será expandido ao longo da variável livre.
Passo 2
No nosso caso temos
Que é essa curva no plano ZY ,
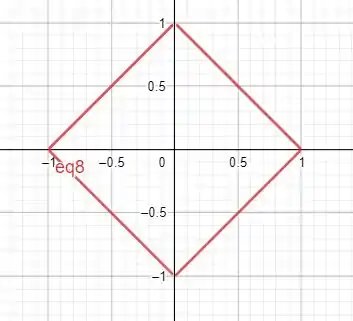
E tem o seguinte formato em 3 Dimensões.
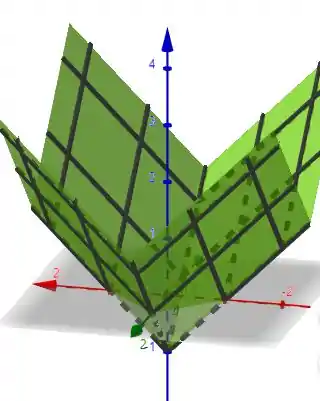
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)