Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.1 - Ex. 3

A figura abaixo mostra a curva de posição versus tempo para uma certa partícula se movendo ao longo de uma linha reta. A partir do gráfico, obtenha uma estimativa para as seguintes quantidades:

  1. A velocidade média no intervalo 0 ≤ t ≤ 3 .
  2. Os valores de t nos quais a velocidade instantânea é zero.
  3. Os valores de t nos quais a velocidade instantânea é máxima ou mínima.
  4. A velocidade instantânea quando t = 3 s.

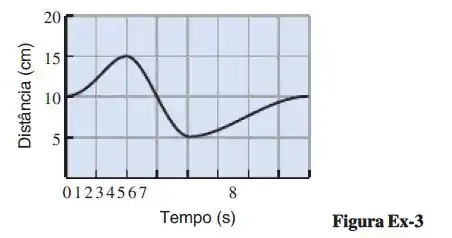
Passo 1

  1. Para achar a velocidade média no intervalo 0 ≤ t ≤ 3 temos a fórmula do deslocamento dividido pelo tempo decorrido:

    2. v m = f t 0 + h - f t 0 h

    O deslocamento é calculado pelo ponto final menos o ponto inicial, e temos o intervalo de tempo, assim vamos substituir:

    v m = f t 0 + h - f t 0 h = 1 0 - 1 0 3 - 0 = 0 3 = 0

    Passo 2

  2. A velocidade instantânea é zero se a inclinação da reta tangente é igual a zero, quando ela é horizontal. Assim temos que a reta tangente é horizontal nos pontos:

    3. t = 0 , t = 2 , t = 4 e t = 8

    Passo 3

  3. A velocidade instantânea é máxima se a reta tangente é bem inclinada e crescente, e vemos no gráfico que é em:

    4. t = 1

    E a velocidade instantânea é mínimo se a reta tangente é bem inclinada e decrescente, e vemos no gráfico que é em:

    t = 3

    Passo 4

  4. Aqui a velocidade instantânea em t = 3 é a inclinação da reta tangente em t = 3 , e podemos achar a inclinação da forma:

m t a n = v = f x 1 - f x 2 x 1 - x 2

Vamos então pegar os pontos:

3 , 1 0 e 4 , 5

Substituindo:

m t a n = v = f x 1 - f x 2 x 1 - x 2 = 1 0 - 5 3 - 4 = 5 - 1 = - 5

Resposta

  1. v m = 0 cm/s
  2. t = 0 , t = 2 , t = 4 e t = 8
  3. Máxima em t = 1 e mínima em t = 3
  4. m t a n = - 5 cm/s
Ver Outros Exercícios desse livro